Problem Set 5 Blood
Goals: back-of-the-envelope estimation, scale, google search
Many complex problems in biology can be broken down into a series of smaller problems and a common smaller problem is the estimation of some number, such as the number of bacteria per cell. Estimation problems range from back-of-the-envelope estimations that are imprecise but useful in that they give one a general sense of the magnitude of a phenomenon to more precisely modeled estimates that are used for making decisions under uncertainty. Back-of-the-envelope estimations are called that because most can, literally, be done with a pencil and the back of an envelope. They can be done with pencil because the computations uses rounded instead of exact numbers like 10 or 300 that are easily multiplied/divided. In this module, you will compute some back-of-the-envelope estimations.
A problem like “how many bacteria can colonize a cell” depends on the distribution of the sizes of the bacteria, the size of the cell, and how packed the cell is with its own molecules and organelles. Here, I simply want to get you started on addressing a problem like this with very simple models of the problem. Along the way, solving the problem should give you a sense of scale of what it is like to be a bacterium or a virus living in a cellular world.
5.1 How to solve an estimation problem
I’ll solve an analogous problem: How many beach balls can fit in a barn? If a barn has Volume Vbarn and a beach ball has volume Vball then the number of balls that could fit into the barn would be approximately, Nballs=VbarnVball. To solve this, I need to paramaterize the model by assigning numbers to these variables. And, the answer is dependent on what numbers I choose for the size of the beach balls and the shape and size of the barn and how filled the barn is with hay (or furniture or horses or whatever) – that is how much of the volume of the barn is available for beach balls. A back-of-the-envelope calculation simply uses a reasonable value for the parameters. So, here are my numbers.
- the barn is a typical vermont barn. I have a sense of what “typical” is because I live in New England and see barns every day. But what if I were a martian, and had never seen a barn? Then I would need to find this information from a reliable source. So, to find “typical”, I used a google search and found what looks like a reputable source that says a typical hay barn is 30 feet wide by 40 feet long. I estimated wall height from the figure as half the width and I used a 12/12 pitch for the roof, so the peak is centered and 15 feet (half of the width) high.
Again – if you don’t have to look up information to parameterize your model, don’t!
I used a big beach ball of 2 feet in diameter (because big beach balls are fun). I didn’t need to look this up!
10% of the barn is filled with hay.
I use Google Sheets to compute the number of balls for each room (the main room and the attic) and then add these. Here is my sheet
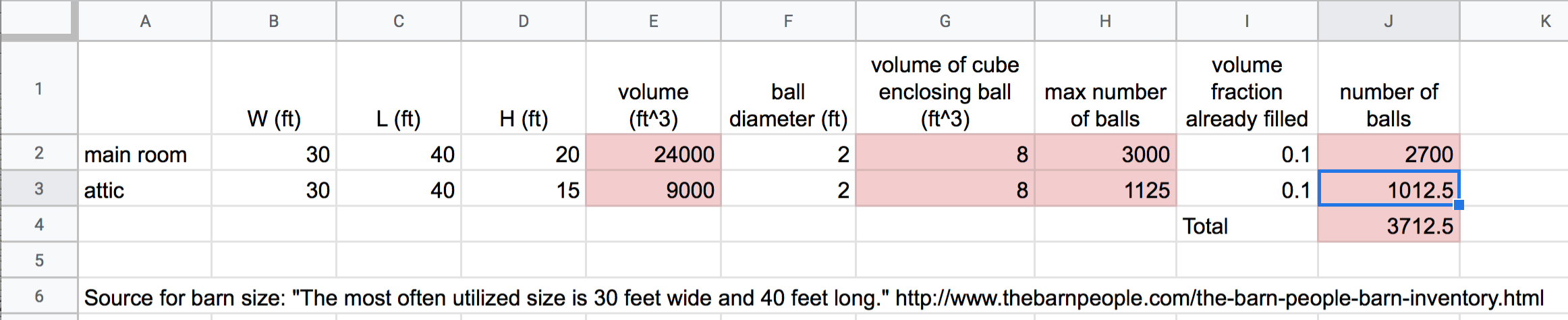
Figure 5.1: Estimation of maximum number of beach balls that could colonize a barn. Cells in red are computed.
My column labels include the units of the measure. Do not add units to the measure itself because this makes the format of the cell “text” instead of “number” and you cannot refer to the cell in an equation. I also cite the source of the parameterization below the table (I cite the source for the size of the barn. The size of the beach ball I just made up).
5.2 Problem set
Do these on the same sheet. Name the sheet “1. Blood”.
- How many red blood cells in a drop of blood? Note, I don’t want you to look up how many RBCs are in a drop, I want you to estimate it using a back-of-the-envelope estimation. You don’t need to look up the volume of a drop of water if you are able to use available information in your head to derive a reasonable volume for a drop of water.
For the next three questions, assume the host cell is “empty”, that is, it contains no organelles or molecules that take up space.
How many bacteria could colonize a red blood cell?
How many bacteria could colonize a macrophage?
How many virus particles could colonize a red blood cell?
– These should all be on the same google sheet.
– Do not hardcode parameters, that is, if a virus is 30 feet wide do not put “30” in an equation but instead make your equations reference the cell with this information.
– You may need to google search information to parameterize the model, such as, how big a virus is. Part of the goal of this is for you to develop your skills finding reliable information using a google search. There is variation in virus size or cell size so use something in the middle or “typical”. Again – these are back-of-the-envelope estimates so you don’t need to be very precise – in fact all of these problems could be computed by most working biologists without looking up any information. We all have a pretty good sense for how big a virus, a bacterium, a blood cell, and a drop of water is. But you can look up this information because you are at the beginning of your biology career.
– Cite a webpage giving the source of the information, as I’ve done for the barns. There is no “right” or “wrong” place to get this information, only more or less reliable. I’m not grading you on where you get it, but I want to see where you get it! And all I want for a citation is the webpage, this is not a formal citation that you put in a scientific paper.