Chapter 3 Material Properties

3.1 The skeleton includes all the structures that function to absorb energy without breaking or permanently deforming, to transfer energy from one part to another, or to store-and-release energy
Most people (even many biologists!) think only of the bones when they think of the skeleton but skeletal structures include any structure that functions to support and physically protect the body and to transfer, store, or absorb mechanical energy. For animals generally, and vertebrates specifically, the skeleton includes the bones and other mineralized tissues, cartilages, tendons, ligaments, the dermis of the skin, and the connective tissues of the walls of the heart, the blood vessels, the respiratory tubes, and other fluid filled tubes in the body. Even fluids can sometimes act as skeletal elements (a hydrostatic, or hydrostatic skeleton). And, while the bones of vertebrates are part of the skeleton, as organs, the bones have other, non-skeletal, functions, for example Ca and PO homeostasis, the storage of fatty acids, and the site of the development of blood cells. In plants, all plant cell walls act as skeletons at the cell level but certain cells organize into distinct skeletal tissues, including collenchyma cells in growing parts of the plant, sclerenchyma cells called fibers, and xylem cells (including the wood in woody plants).
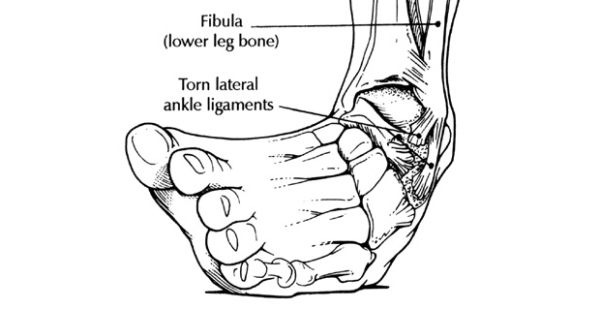
Figure 3.1: Inverted ankle joint
A vertebrate skeleton has to do lots of things. Hyena’s crush the bones of scavenged prey to get to the fatty marrow inside. When crushing a bone, the hyena’s teeth, mandible (the bone of the lower jaw), and maxilla (a bone of the upper jaw) need to transfer the force of muscle contraction to crack the prey bone. Imagine if hyena teeth were made of rubber, like a solid rubber ball. When biting bone, their teeth would simply be squished (or compressed). Instead the bones of the jaw and the teeth need to resist deformation, or shape change, in order to transmit the force.

Figure 3.2: Some tendons or ligaments act like springs
Unlike humans, most vertebrates run on uneven surfaces filled with rocks, roots, and small depressions and mounds. Landing on an uneven surface will frequently put the ankle joint into bending, which applies a force that stretches ligaments on the convex side of the bent ankle (figure~). A tight (difficult to stretch) ligament inhibits excessive bending and thus maintains joint stability. But in addition to be unstretchy, the ligament needs to be tough, to keep from tearing.
An under-appreciated function of the vertebrate skeleton, especially in introductory textbooks, is the ability of some skeletal structure to act like a spring. Squash or stretch a spring and it springs back to its starting length and this spring can be used to do work on something, such as launching a man, or a kangaroo, against gravity. In the vertebrate body, the skeleton of many structures act like springs and are used to reduce the energy cost of activity, such as hopping in kangaroos. Unlike skeletal structures used for transmitting forces or resisting deformations, structures that act like springs should be easily stretch or squashed.
The ability of a structure to resist stretching, or bending, or breaking is a function of both the geometry of the structure (its size and shape) and of the material in the structure. In this chapter, we will focus on the latter – the material properties.
3.2 Skeletons are loaded by external forces
We use the term load when we say that a pressure (or force) is applied on an object. When we stand, our femur is loaded by the weight of our upper body pushing down onto the femur and the earth pushing back up. Loads come in differ flavors, or loading environments:

Figure 3.3: Apatosaurus
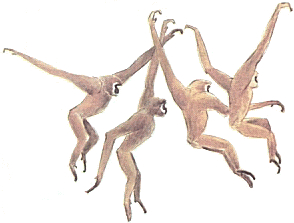
Figure 3.4: Gibbon brachiation
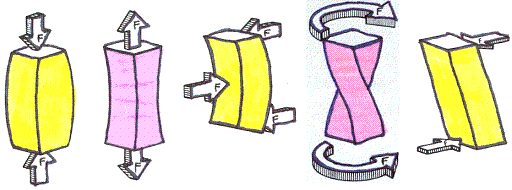
Figure 3.5: Can you identify the type of loading in each of these structures?
- Compression has the effect of squeezing a structure. When an Apatosaurus stands, the limbs are loaded in compression because the weight of its (large!) body is pushing down on the limbs and a reactive force from the earth is pushing back up. That is, the limbs are squozen.
- Tension has the effect of stretching a structure. When a gibbon hangs from a tree limb, its humerus, radius, humeroulnar joint, and wrist joint are all loaded in tension. These are being pulled apart because the gibbon’s body weight is pulling these structures one way and the tree limb is pulling equally and oppositely in the other direction.
- Bending has the effect of bending a structure. The vertebral column between the front and hind limbs of the Apatosaurus is loaded in bending because the earth/limbs are pushing up at the ends of the column and the weight of the torso is pulling down the middle of the column.
- Torsion has the effect of twisting a structure. When a gazelle fleeing a cheetah turns on a dime, the limbs are loaded in torsion because the torso is turning to the side but the ground is resisting the limbs from spinning.
- Shear is the force due to materials sliding by each other. Shear is important in the joints where the ends of bones slide past each other and in the blood, where the moving blood loads the wall of the blood vessel in shearing.
3.3 Stress in a material is the resistance to strain
When a force is applied to an object, the object deforms (often so little that we cannot see the deformation!). How an object deforms is really critical to its function in an organism. In order to understand how material properties determine why some objects are very resistant to deformation while others easily deform, or why some objects are resistant to fracture while others are easily fractured, or why some structures increase the efficiency of cyclical motions while others don’t, we need to separate the effects of the geometry (in general size but sometimes shape too) of the object from the material of the object. The size of the object is standardized by dividing by the force () by the cross-sectional area () of the object that is loaded and dividing the change-in-length (, the deformation) by the starting length (). This results in two really fundamental parameters:
- strain is the standardized deformation, . There are no units, that is, is dimensionless
- stress is the standardized force resisting deformation, and has SI units of , which are the units of pressure.
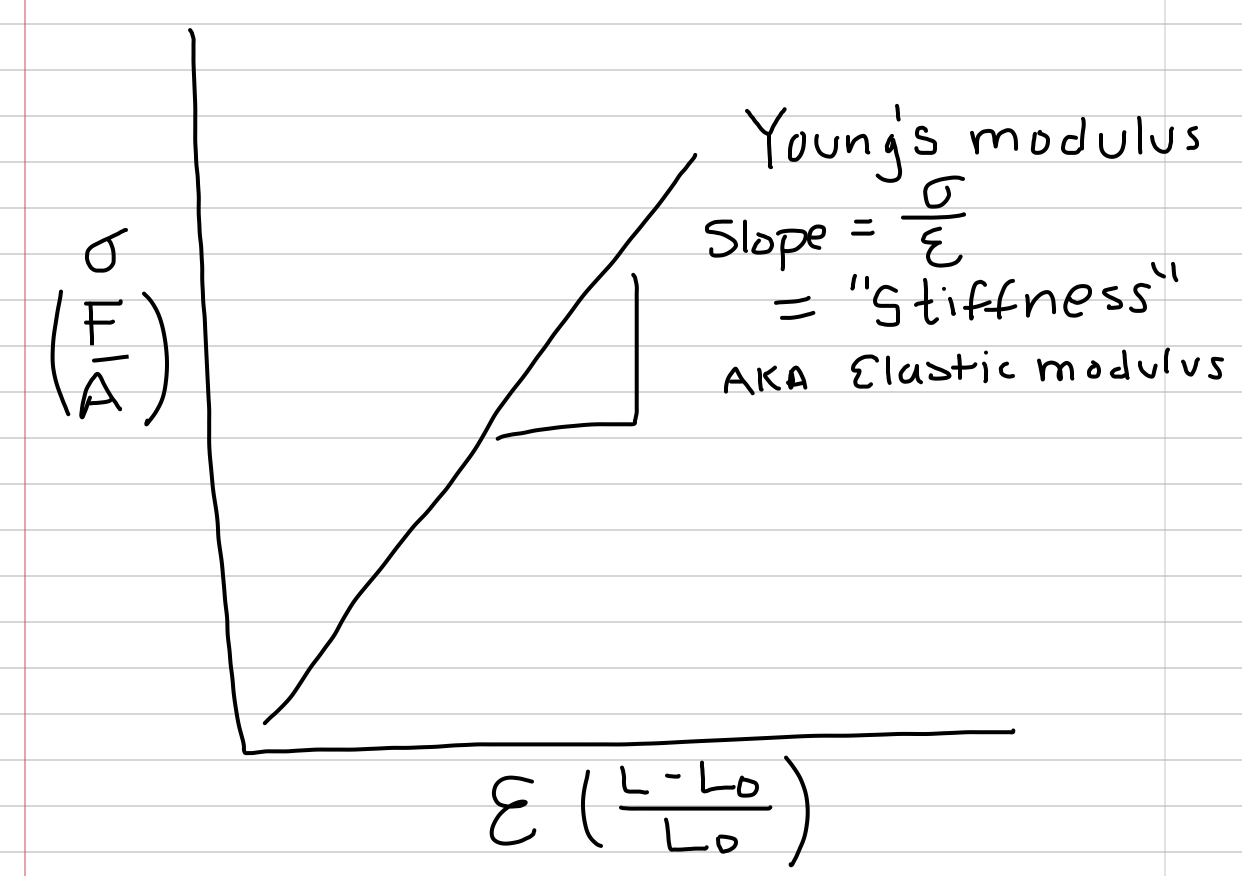
Figure 3.6: A somewhat idealistic stress-strain curve
Stress is not the pressure applied to the structure but the area-standardized reaction force of the material in response to the external load. Stress is the reaction to strain. Or, stress is the intrinsic resistance to strain. Deformation (strain) causes a rearrangement of the atoms in a material. The rearranged atoms are attracting/repelling each other in a way that will return the material toward its starting length if the external load is removed. Stress is this internal, standardized force due to the atoms attracting/repelling each other. If the external load is removed from a deformed material, there is still stress, and this stress is present until the added attraction/repulsion force returns to their starting value. So while an external load causes strain, strain causes stress! Importantly, all of the loading environments described above can be applied to stress as well, so that we use the phrase “tensile stress”.
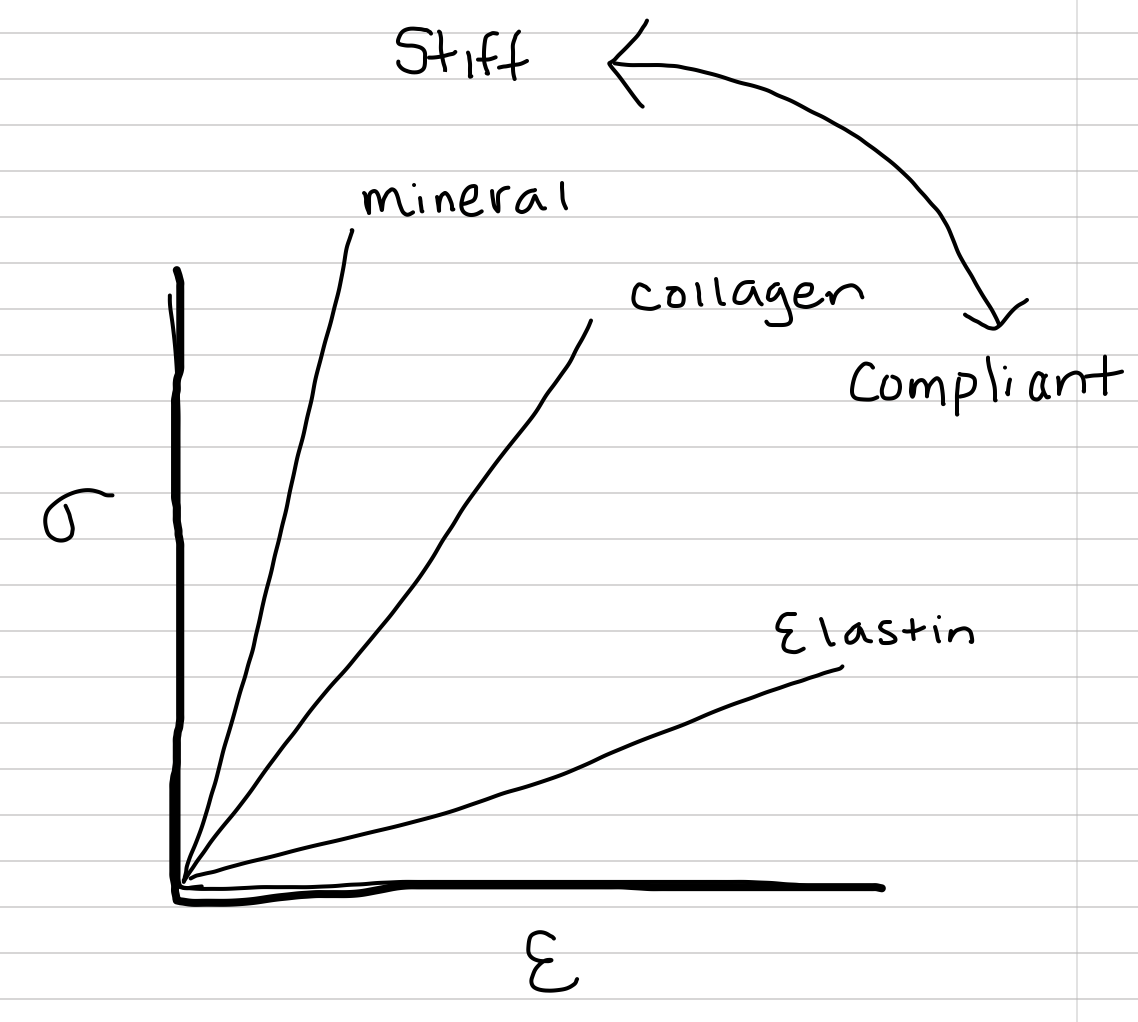
Figure 3.7: Relative stress-strain curves for hydroxyapatite, collagen, and elastin
This ability of a material to resist deformation is graphically shown by the slope of a stress-strain curve, with stress () on the y-axis and strain on the x-axis. This slope is called the Elastic (or Young’s) Modulus (), or stiffness. Since the curve starts at the origin (0, 0), the elastic modulus is
Materials with high (steeper slopes) are stiff, materials with low (shallower slopes) are compliant. Mineralized tissue is stiff relative to a tissue with abundant collagen which is stiff relative to a tissue with abundant elastin (we can’t really test individual proteins). Rubber in a rubber band is more compliant than nylon used for rope.
3.4 Work has to be done on a structure to deform it and generate stress
It takes mechanical work to deform a material. Mechanical work is a form of energy used to move an object a certain distance, . The standard example in physics is pushing a box across a floor. But when the weight of an Apatosaurus deforms its femur (the bone of the thigh), it’s not the whole femur that is moving through space but the individual atoms within the femur. All of these microscopic movements sum up to the total amount the bone shortens under the compressive load, . is the in the equation for mechanical work.
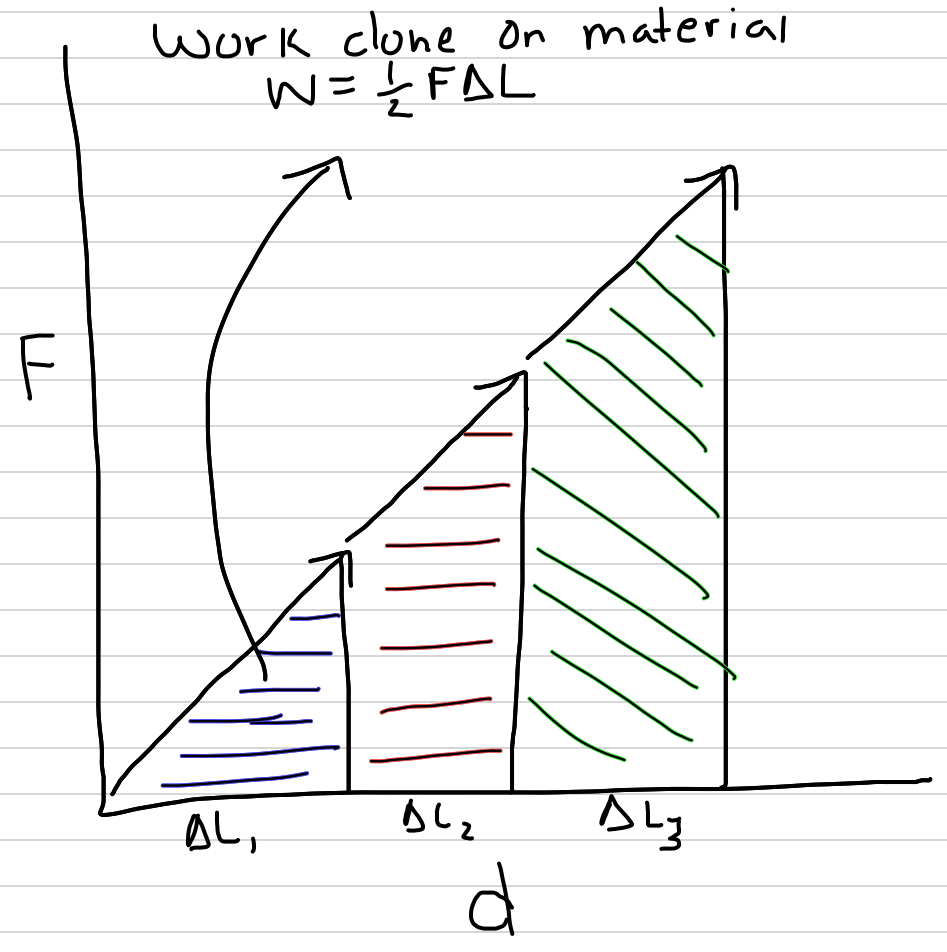
Figure 3.8: The area under the force-deformation (not stress-strain!) curve at any level of deformation is the work done to deform the material. This energy is transferred to the material.
How much work does it take to deform a structure? Imagine clamping a cut-out piece of the wall of the aorta to a board and then clamping a weight to the aorta and measuring . then repeat this for a series of larger and larger weights, but instead of computing as the difference between the current length and starting length, compute it as the difference between the current length and the length with the previous, smaller weight, so . An approximate measure of the additional work done on the aorta wall to deform it this additional , is and an approximate measure of the total work done to deform the aorta from its starting length is .
Additional insight is gained by plotting each of the weights () against the added deformations () using the non-standardized measures (at this point, these are not standardized to stress and strain). The measure of each of the components of Work, that is, the , is the area of a rectangle with height and width . And, the total Work is an approximate measure of the area under the curve connecting the measured points. The more weights one uses to measure this line, the closer the approximate measure of Work is to the area under the curve. The area under the curve is the actual work done on the aorta wall. If this curve is a straight line, the Work to deform the aorta is .
3.5 Materials absorb strain energy
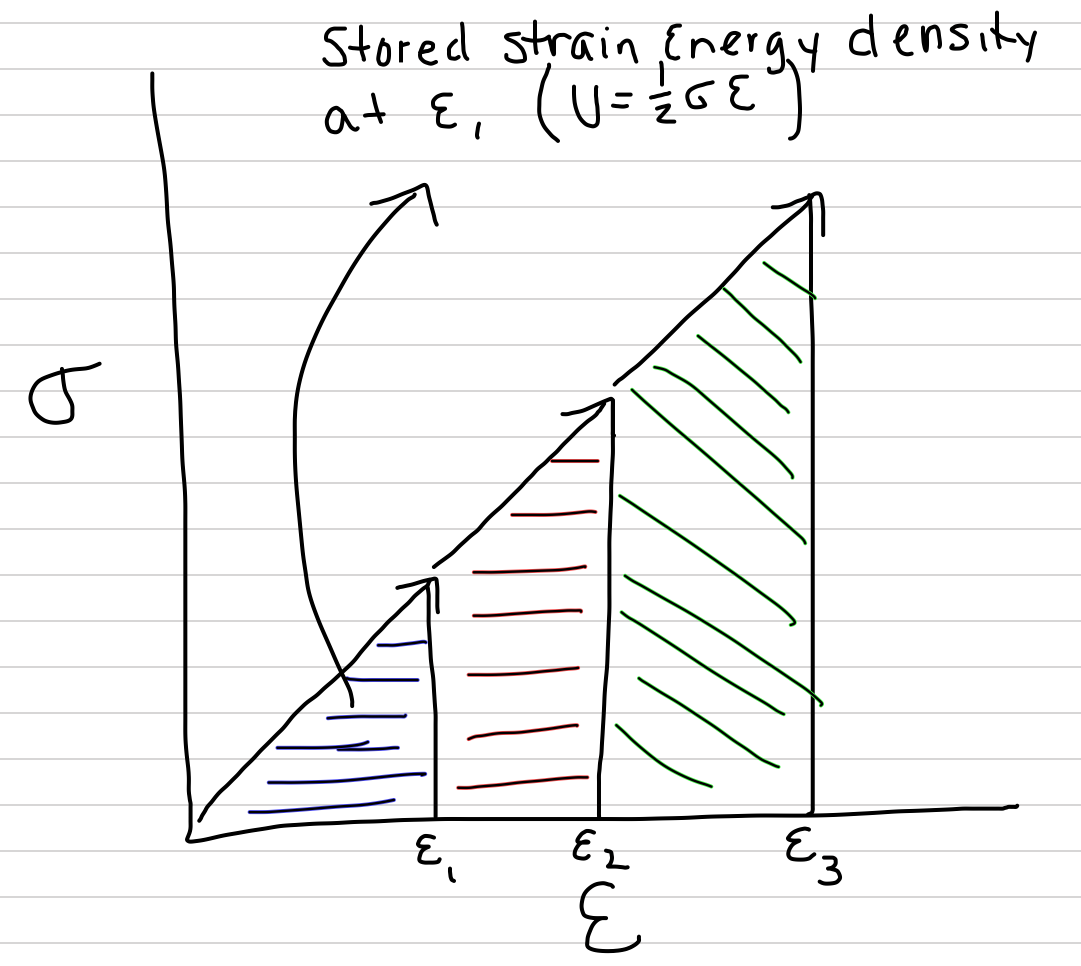
Figure 3.9: The area under the stress-strain curve at any level of deformation is the strain-energy density (the strain energy per unit volume) that is stored.
Doing work on a structure transfers energy into the structure. This absorbed energy rearranges the atoms in the material. Or, we can think of these rearranged atoms as absorbing or storing the energy. This stored energy is known as strain energy. The magnitude of the strain energy will be a function of both the geometry of the structure and the type of material in the structure. So, to remove the influence of geometry on this measure, we used the scaled force and deformation, and . For a straight stress-strain curve, this standardized energy is
Substitute in the equations for stress and strain and this standardized energy is
The numerator of this equation is the mechanical work done on the object, which is also the strain energy absorbed by the material. The denominator is the volume of the starting object. Consequently, is volume-standardized strain energy, or strain energy density (this is the energy stored per unit volume in analogy to density, which is the mass per unit volume).
3.6 Stored strain energy can do work
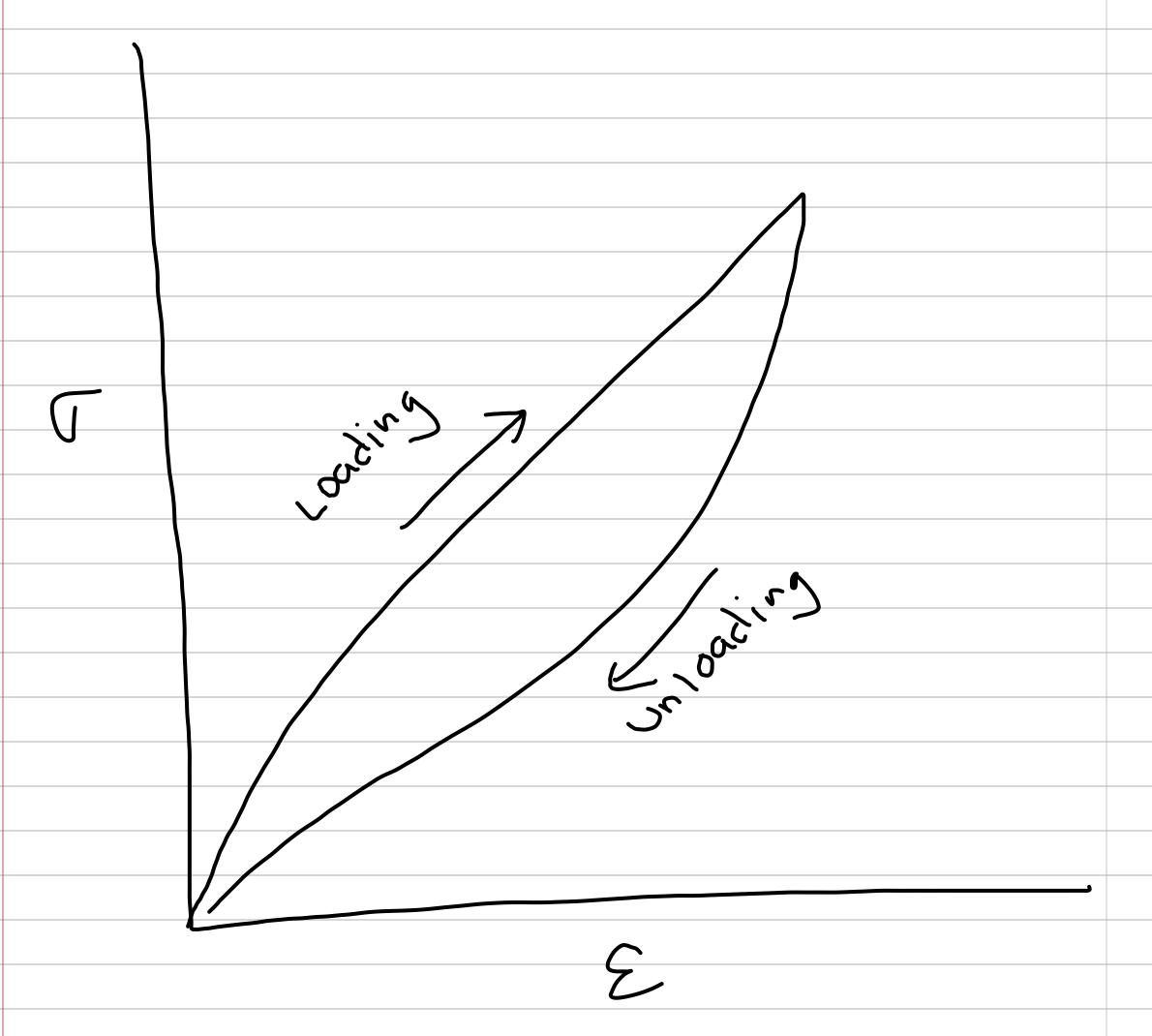
Figure 3.10: The loading curve is the behavior while a material is being deformed by some load. The unloading curve is the behavior when the load is removed.
If the external load is removed, the stored strain energy does work on the surrounding material, moving the atoms back toward their starting arrangement. In an elastic material, which includes most biological materials that aren’t fluid, the starting length is completely recovered. If the surrounding material includes an another object, some of the stored energy is transferred into that object, typically as kinetic energy (if the object is put into motion). This storage and release of elastic strain energy has profound implications for both human engineering and for animal function. For human-engineering, think of sling-shot. Energy from moving limbs is transferred into the rubber material of the sling as strain energy. The strain energy is used to return the sling to its starting length and the energy of this return motion is used to shoot a rock. Animal bodies are full of structures that store and release elastic strain energy. For example, during lung ventilation in mammals, our thorax cycles between inspiration (the inhale) and expiration (the exhale). Contraction of the diaphragm muscle powers inspiration: the diaphragm contracts, the thoracic volume increases, which depresses alveolar air pressure, which sucks air into the alveoli through an open mouth and nose. The expanded thoracic wall and lung itself store elastic strain energy. When the diaphragm relaxes, this stored strain energy powers expiration. The total energetic cost of ventilation is markedly reduced because of the ability of thoracic tissues to store and release elastic strain energy.
3.7 The work that a strained material can do is always less than the work done to deform the material
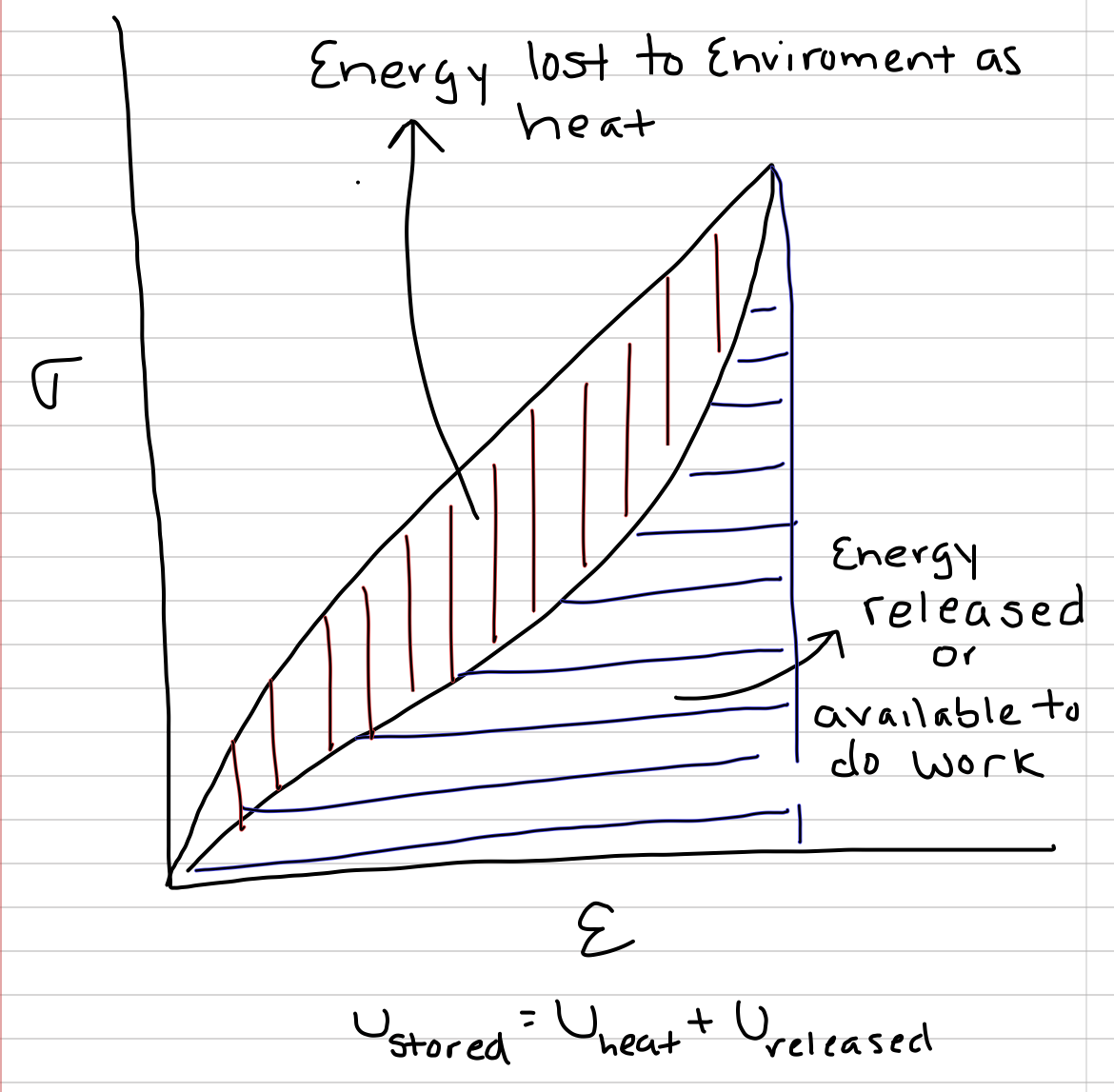
Figure 3.11: The total area under the loading curve is the stored elastic strain energy density. The area under the unloading curve is the fraction of stored elastic strain energy density that is returned, or available to do work. The area between the two curves is the fraction of stored elastic strain energy density that is lost to the environment as heat
The stress-strain curve measured while unloading a material is always depressed relative to the curve measured while loading the material. The area under the loading curve is volume-standardized work done on the material (so the actual work is this number times the volume of the material). This volume-standardized work is equal to the stored strain-energy density. The area under the unloading curve is the fraction of the stored strain-energy density that is available for doing mechanical work on surrounding matter. This released elastic strain energy is always less than the stored elastic strain energy. The difference between the stored energy and the released energy is transferred to the environment as heat.
3.8 Material Properties determine if a tissue is good at absorbing strain energy without breaking or storing and releasing lots of elastic strain energy
Figure 3.12: Illustration of material properties. Strength is the maximum stress without failure. Deformability is the maximum strain without failure. Stiffness is the elastic modulus and is the slope of the curve. Toughness is the area in red. The input (absorbed) strain energy density is the hatched area. The output (released) strain energy density is the dotted area. The hatched area without dots is the amount of heat produced when the elastic material returns to its starting length. Resilience is the ratio of output to input strain energy density.
These material properties are
- Stiffness, aka the Modulus of Elasticity, the Elastic Modulus, or Young’s Modulus, is the slope of the stress strain curve, which is for a material with a linear curve. is a measure of the resistance to deformation. I usually just refer to this measure as the material’s . The more force it takes to deform a material a certain amount, the higher the elastic modulus. Or from the view of the material, the elastic modulus is high if only a small strain creates a high stress. A material with a high elastic modulus is stiff. The opposite, a material with a low elastic modulus, is compliant. Compliant materials are easily stretched or squished.
- Strength, or breaking strength, or tensile strength (if in tension), is the maximum stress that a material can resist without , or breaking. A strong material can withstand high stress before failure. The opposite is weak.
- Deformability is the strain of the material at failure. If the material is in tension, this is extensability. All highly deformable materials are compliant but not all compliant materials are highly deformable.
- Toughness, T, is the strain energy density at failure. Materials that can absorb lots of strain energy are tough. The opposite is brittle. Stiff materials tend to be brittle. More compliant (but not too compliant!) materials tend to be tough. Bones used for support (and the wood of tree trunks) must be tough in addition to being strong.
- Resilience, R, is the percent of the total absorbed strain energy that can be used to do work and so is the ratio of the released strain energy (, the area under the unloading curve) to the total absorbed strain energy (, the area under the loading curve). This ratio is always less than one (otherwise a ball made of a material with a resilience of one could bounce forever!). The ability of a tissue to store-and-release elastic strain energy is a function of both resilience and compliance. Collagen and elastin are both very resilient but collagen is also much stiffer than elastin.