2.4 Work has to be done on a structure to deform it and generate stress
It takes mechanical work to deform a material. Mechanical work is a form of energy used to move an object a certain distance, . The standard example in physics is pushing a box across a floor. But when the weight of an Apatosaurus deforms its femur (the bone of the thigh), it’s not the whole femur that is moving through space but the individual atoms within the femur. All of these microscopic movements sum up to the total amount the bone shortens under the compressive load, . is the in the equation for mechanical work.
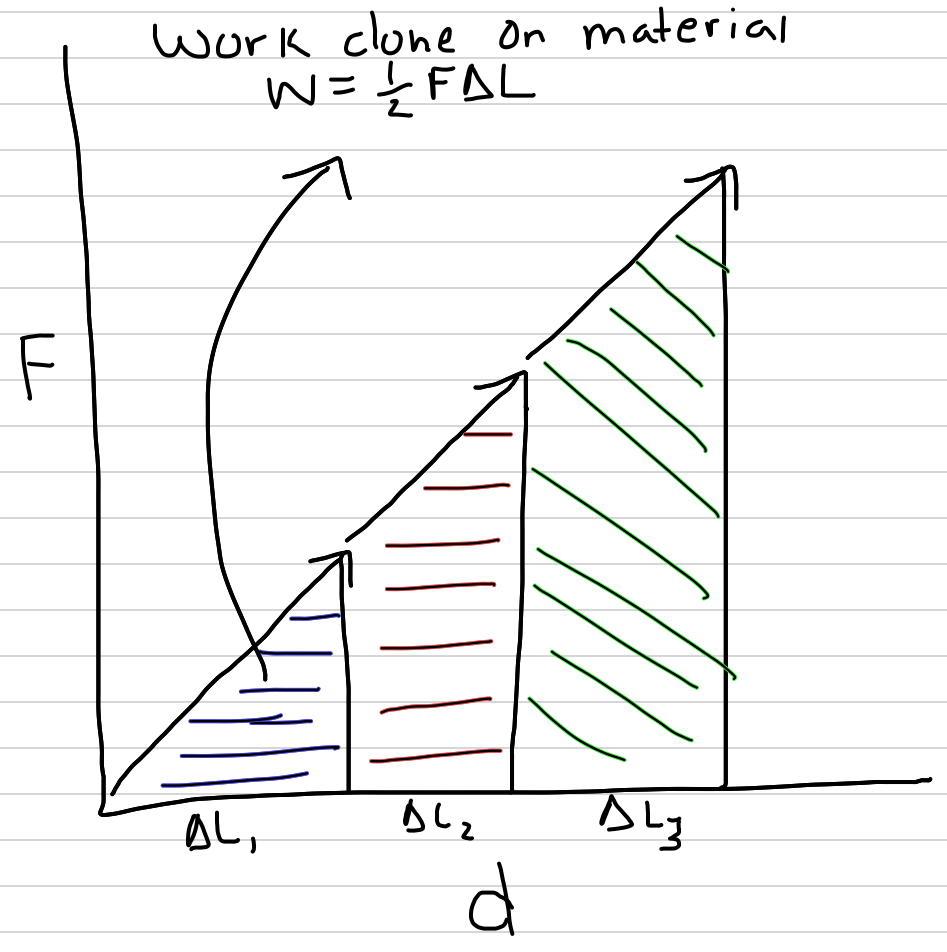 Figure 2.8: The area under the force-deformation (not stress-strain!) curve at any level of deformation is the work done to deform the material. This energy is transferred to the material.
Figure 2.8: The area under the force-deformation (not stress-strain!) curve at any level of deformation is the work done to deform the material. This energy is transferred to the material.
How much work does it take to deform a structure? Imagine clamping a cut-out piece of the wall of the aorta to a board and then clamping a weight to the aorta and measuring . then repeat this for a series of larger and larger weights, but instead of computing as the difference between the current length and starting length, compute it as the difference between the current length and the length with the previous, smaller weight, so . An approximate measure of the additional work done on the aorta wall to deform it this additional , is and an approximate measure of the total work done to deform the aorta from its starting length is .
Additional insight is gained by plotting each of the weights () against the added deformations () using the non-standardized measures (at this point, these are not standardized to stress and strain). The measure of each of the components of Work, that is, the , is the area of a rectangle with height and width . And, the total Work is an approximate measure of the area under the curve connecting the measured points. The more weights one uses to measure this line, the closer the approximate measure of Work is to the area under the curve. The area under the curve is the actual work done on the aorta wall. If this curve is a straight line, the Work to deform the aorta is .