Chapter 16 Models for non-independence – linear mixed models

Probably no chapter in this book is more important for the best-practice analysis of experimental data than this chapter. Why? Because many if not most experimental data violates the assumption of independence and any analysis using standard t-tests and ANOVA will always lead to quantitative error in inference (confidence intervals and p-values) and often lead to qualitative errors in inference (statements about “significance”). Standard analysis of non-independent data can lead to absurdly liberal inference (the p-values are far lower than the data support), but can also lead to moderately conservative inference (the p-values are higher than the data supports). Liberal inference generates false discovery and lures researchers down dead-end research pathways. Conservative inference steers researchers away from true discovery.

Linear Mixed Models are an extension of linear models that appropriately adjust inferential statistics for non-independent data. Paired t-tests and Repeated Measures ANOVA are classical tests that are special cases of linear mixed models. Linear mixed models are more flexible than these classical tests because the models can include added covariates or more complex models generally. And, linear mixed models can be extended to Generalized Linear Mixed Models for counts, binary responses, skewed responses, and ratios.

Before introducing experimental designs that generate non-independent data and the models used to analyze these, let’s explore two ubiquitous examples, one that leads to liberal inference and one that leads to conservative inference.

16.1 Liberal inference from pseudoreplication

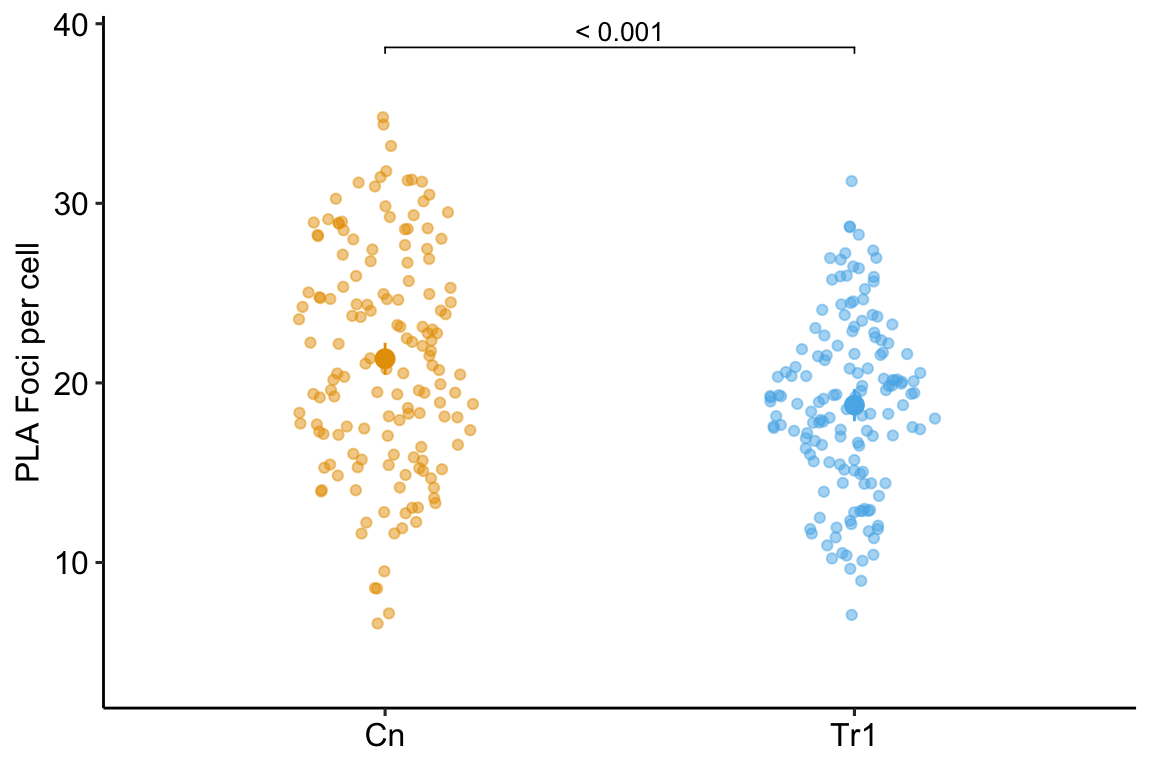
Researchers are interested in regulation and repair of DNA double-stranded breaks and use a proximity ligation assay (PLA) of HeLa cells to investigate the number of damage response events (“foci”) per cell with and without an inhibitor of transcription elongation (DRB). The number of foci in each of fifty cells per treatment is measured. The experiment is replicated three times. The researchers use a t-test to compare the effect of DRB on foci count and naively include all measures in the analysis.

What is naive about the analysis? The fifty measures per cell are technical replicates and the values within a cell are not independent of each other because they share aspects of cell environment not shared by values in other cells. Including technical replicates in an analysis without accounting for this non-independence is a kind of pseudoreplication

To show how this naive analysis results in extremely liberal inference and an increase in false discovery, I simulate this experiment using a case in which there is no effect of DRB treatment, so a low p-value indicates a false-discovery. The simulation is simplified with the two following conditions: 1) the model pretends that count data are normally distributed (this is because we want to focus on pseudoreplication and not a misspecified distribution) and 2) the model pretends that values from each treatment within an experiment are independent (this is because we want to focus on pseudoreplication).

In this naive analysis of the experiment, the researcher finds an effect of treatment with a p-value of 0.000073 and uses this small p-value to justify a decision to move forward with follow-up experiments. But this low p-value is not supported by the data – this discovery is false. This very small p-value is not an example of a “rare event”. In fact, if the researcher repeats the experiment 1000 times, then the median p-value is 0.000195 and 72.3% of the 1000 p-values lead to the same false discovery if 0.05 is used to make the decision to move forward.

While this example is fake, I see this naive analysis a lot: tumor area of multiple tumors per mouse, islet area of multiple islets per mouse, number of vesicles docked to a membrane in multiple cells per mouse, the number of mitochondria in multiple cells per mouse, the number of neurites in multiple neurons in multiple cells per mouse, etc. etc. Indeed, when I’m looking for examples of pseudoreplication to teach, I just look for figures with a bunch of points per treatment – something similar to this plot of the fake data experiment. Regardless, this is a huge source of false discovery that could disappear overnight.

16.2 Conservative inference from failure to identify blocks

Researchers frequently divide a litter among treatment levels (“littermate control”) but only once have I seen researchers use this design to increase statistical power and decrease the rate of failed discovery. Here is a fake data example. Researchers are interested in sensory regulation of wound healing and use the Nav1.8cre/Rosa26DTA mouse model to investigate the role of dorsal root ganglion (the location of peripheral sensory neuron cell bodies) in this management. Two mice from each of six litters are sampled, one Nav1.8cre sib with an ablated dorsal root ganglion and one Rosa26DTA “littermate control” with an intact dorsal root ganglion. The researchers use a naive t-test to compare the effect of ablation on muscle area (12 days after wounding).

What is naive about the analysis? Each mouse is a block and the values within a block are not independent of each other because they share aspects of genetics and maternal environment not shared by values in other blocks (mice). In general, variation among blocks (mice) adds correlated noise to data and failure to account for blocks will often lead to more conservative inference.

To show how this naive analysis results in conservative inference and an increase in failed discovery, I simulate this experiment using a case in which there is an effect of ablation treatment, so a low p-value indicates a true discovery.

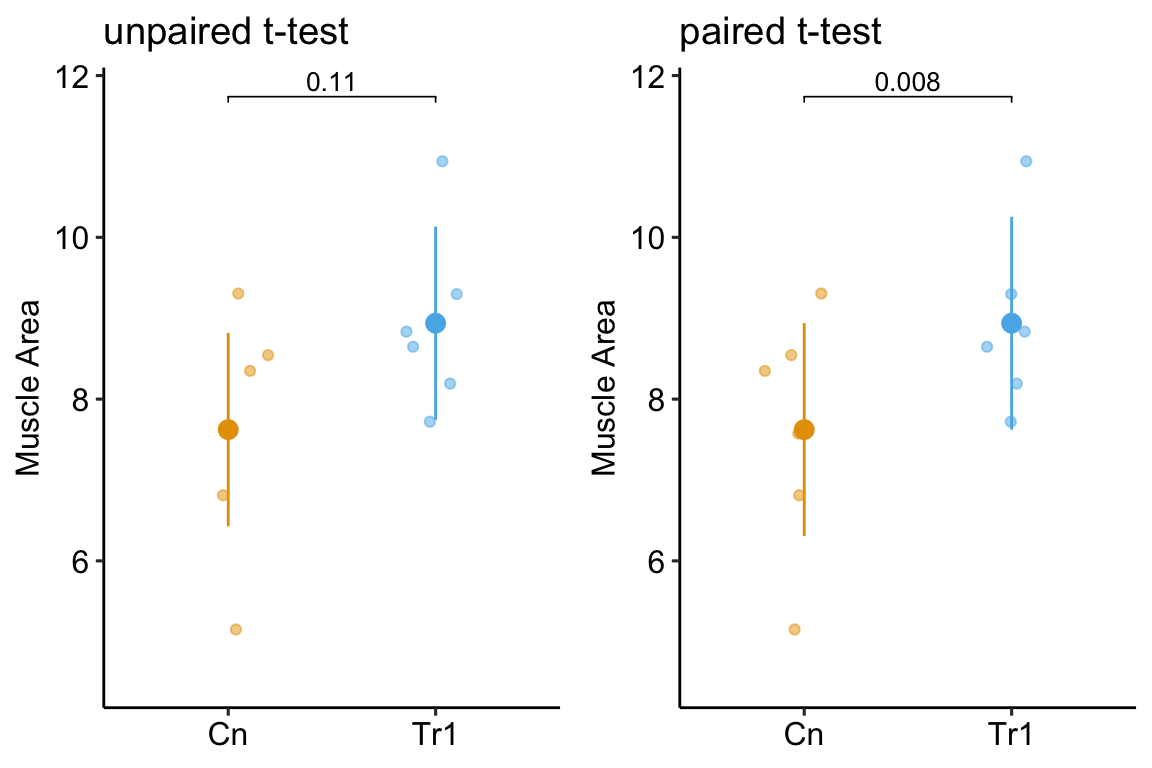
In this naive analysis of the experiment, the p-value of the treatment is 0.26 and uses this large p-value to put the grad student onto a different project. Too bad, because the effect is real. The p-value from a paired t-test (the values of the two mice within a litter are a pair), which is equivalent to a special case of a linear mixed model, is 0.0012. This small p-value using a model that accounts for the non-independence is not an example of a “rare event”. In fact, if the researcher repeats the experiment 1000 times, 72.5% of the paired t-test p-values are less than 0.05 while only 12.1% of the classical t-test p-values are less than 0.05.

While this example is fake, I see this naive analysis a lot – littermate controls is very, very common but other examples are too, included replicated experiments (each experiment is a block). There are certain instances where researchers do recognize non-independence and do use a paired t-test but the vast majority of blocked designs (occurring in almost all experimental biology papers) go unrecognized. This is a huge source of failed discovery that could disappear overnight.

16.3 Introduction to models for non-independent data (linear mixed models)

This chapter is about models for correlated error, including linear models with added random factors, which are known as linear mixed models. In classical hypothesis testing, a paired t-test, repeated measures ANOVA, and mixed-effect ANOVA are equivalent to specific cases of linear mixed models. Linear mixed models are used for analyzing data composed of subsets – or batches – of data that were measured from the “same thing”, such as multiple measures within a mouse, or multiple mice within a litter. Batched data results in correlated error, which violates a key assumption of linear models (and their “which test” equivalents) and muddles statistical inference unless the correlated error is modeled, explicitly or implicitly. In some experimental designs (blocked designs), failure to model the correlated error reduces precision and power, contributing to reduced rates of discovery or confirmation. In other designs (nested designs), failure to model the correlated error results in falsely high precision and low p-values, leading to increased rates of false discovery. The falsely high precision is due to pseudoreplication. I think it’s fair to infer from the experimental biology literature, that experimental biologists don’t recognize the ubiquitousness of batched data and correlated error. This is probably the biggest issue in inference in the field (far more of an issue than say, a t-test on non-normal data).

What do I mean by “batch” and how can correlated error both increase and decrease false discovery? Consider an experiment to measure pancreatic islet area in response to two experimental factors: $\texttt{genotype}$ (WT, KO) and $\texttt{treatment}$ (presence/absence of some drug believed to be an agonist of the knocked out protein). While it may seem like the data from this experiment should be analyzed using the ANOVA option in GraphPad Prism (or, as advocated in this book, a general linear model that is equivalent to the ANOVA), the best practice statistical model actually depends on the experimental design. Experimental design matters because different designs introduce different patterns of correlated error due to shared genetics and environment. Recall that inference from a linear model (including t-tests and ANOVA) assumes independence (Chapter xxx) – that is, each response value has no relationship to any other value, other than that due to treatment. Lack of independence results in patterns of correlation among the residuals, or correlated error.

Something like the first experiment below (Design 1) is the necessary design to use the statistics that have been covered in this book to this point, without extreme violation of the independence assumption. But many (most?) experiments in experimental bench biology do not look like the design in Design 1 below. Instead, many (most?) experiments are variants of Designs 2-4, all of which have extreme violations of the independence assumption. Interestingly, some of these violations result in conservative statistics and reduced, true discovery rate while others result in liberal statistics and increased, false discovery rate.

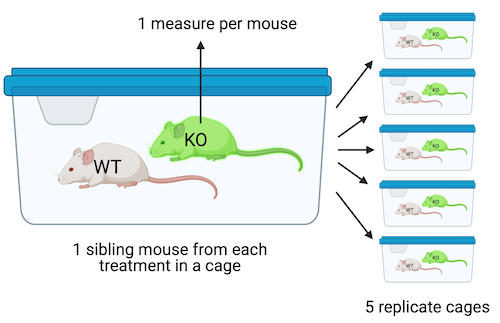
Design 1. The design in Figure @ref(fig:lmm-biological-replicates_1) is a factorial design with two factors, $\texttt{genotype}$ and $\texttt{treatment}$, each with two levels. Twenty mice of the same sex, each from a different litter from a unique dam and sire mating, are randomly sampled and assigned to one $genotype \times treatment$ combination (five mice per combination). All mice are housed individually (20 cages). The pancreatic tissue from all mice is prepared in a single batch and the area of a single islet is measured from each mouse. The entire experiment is carried out at the same time and each component (tissue preparation, measuring) is carried out by the same person (these could be different people for each component). This is a Completely Randomized Design (CRD). The five replicate mice per treatment are treatment replicates (often called biological replicates in experimental biology. A CRD does not have batched data.

Design 2. In the design in Figure ??, four littermates are randomly sampled from five litters, each with a different dam and sire. Within each litter, mice are randomly assigned to each of the four treatment combinations (one per combination). Each litter is randomly assigned to cage with only a single litter per cage. All other aspects of this design are as in Design 1. This is a Randomized Complete Block Design. The five replicate mice per treatment are the treatment replicates. Each litter/cage combination is a type of batch called a block. A blocked design typically functions to reduce noise in the model fit (this increases power) and to reduce the number of litters and cages needed for an experiment. The four measures of Islet Area within a litter/cage (one per mouse) are not independent of each other. Each cage has four mice from the same litter and these mice share genetic and maternal factors that contribute to mouse anatomy and physiology that are not shared by mice in other litters. Additionally, each cage has a unique set of environmental factors that contribute to the error variance of the measure of the response. Each cage shares a cage-specific history of temperature, humidity, food, light, interactions with animal facilities staff, and behavioral interactions among the mice. All response measures within a litter/cage share the component of the error variance unique to that litter/cage and, as a consequence, the error (residuals) within a litter/cage are more similar to each other than they are to the residuals among litters/cages.

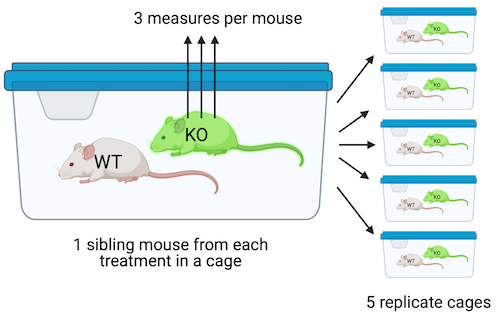
Design 3. The design in Figure ?? is exactly like that in Design 2, except that the researchers take three measures of iselet area per mouse. The three measures are subsampled replicates. Experimental biologists often call these technical replicates, especially when the multiple measures are taken from the same preparation. Subsampling is a kind of nested design in which one variable is nested within (as opposed to crossed with) another variable. Here, the subsampled variable (subsample_id) is nested within the mouse_id variable. In addition to each litter/cage being a batch, each mouse is a batch. Each mouse has a unique set of factors that contribute to the error variance of the measures of the response in that mouse. All response measures within a mouse share the component of the error variance unique to that mouse and, as a consequence, the error (residuals) within a mouse are more similar to each other than they are to the residuals between mice

Design 4. The design in Figure ?? is a variation of Design 2, but the five treatment replicates of each combination are housed together in the same cage. In this design, each litter is a batch and each cage is a batch but these are different batches, unlike Design 2.

In each of these experiments, there is systematic variation at multiple levels: among treatments due to treatment effects and among batches due to batch effects. Batches come in lots of flavors, including experiment, litter, cage, flask, plate, slide, donor, and individual. The among-treatment differences in means are the fixed effects. The among-batch differences are the random effect. An assumption of modeling random effects is that the batches are a random sample of the batches that could have been sampled. This is often not strictly true as batches are often convenience samples (example: the human donors of the Type 2 diabetes beta cells are those that were in the hospital).

The variation among batches/lack of independence within batches has different consequences on the uncertainty of the estimate of a treatment effect. The batches in Experiment 1 contain all treatment combinations. The researcher is interested in the treatment effect but not the variation due to differences among the batches. The batches are nuissance factors that add additional variance to the response, with the consequence that estimates of treatment effects are less precise, unless the variance due to the batches is explicitly modeled. Modeling a batch that contains some or all treatment combinations will increase precision and power.

Batches that contain at least two treatment combinations are known as blocks. A block that contains all treatment combinations is a complete block. A block that contains fewer than all combinations is an incomplete block. Including block structure in the design is known as blocking. Blocks are non-experimental factors. Adding a blocking factor to a statistical model is used to increase the precision of an estimated treatment effect. Design 2 is an example of a randomized complete block design.

In Design 3, there are multiple measures per mouse and the design is a randomized complete block design with subsampling. The subsampling is not the kind of replication that can be used to infer the among treatment effect because the treatment assignment was not at the level of the subsamples. The treatment replicates are the litters/cages, because it was at this level that treatment assignment was randomized. A statistical analysis of all measures from a subsampled design without modeling the correlated error due to the subsampling is a kind of pseudoreplication. Pseudoreplication results in falsely precise standard errors and false small p-values and, consequently, increased rates of false discovery.

In Design 4, the treatment is randomized to batch, so each batch contains only a single treatment level. In these segregated experimental designs, the variation among batches that arises from non-treatment related differences among batches confounds the variation among batches due to a true treatment effect. Design 4 is an extreme example of this – there is only a single cage with a specific treatment combination. Imagine 1) the true effect of a treatment combination is zero and 2) an aggressive mouse in the control cage stimulates the stress response in the other mice and this stress response has a large effect on the value of the response variable measured by the researchers. The researcher is fooled into thinking that the treatment caused the difference in the response.

In all of these designs, it is important for the researcher to identify the experimental unit and the measurement unit. The experimental unit is the entity that was randomly assigned the treatment. In designs 1 – 3, the experimental unit is the mouse. In experiment 4, the experimental unit is the cage. The measurement unit is the entity that was measured. In designs 1, 2, and 4, the measurement unit is the mouse. In design 3, the measurement unit is specific islet that was measured.

Pseudoreplication. In pseudoreplication, the degrees of freedom used to compute the test statistic and the p-value are inflated given the experimental design and research question. An example: A researcher wants to investigate the effect of some protein on mitochondrial biogenesis and designs an experiment with a wildtype (WT) and a conditional knockout (KO) mouse. Mitochondrial counts from twenty cells in one WT mouse and one KO mouse are measured and the researcher uses a t-test to compare counts. The sample size used to compute the standard error in the denominator of the t-value is 20. The t-distribution used to compute the p-value uses 38 df (20 measures times two groups minus two estimated parameters). This is wrong. The df are inflated and the estimate of the standard error of the difference (the denominator of the t-value) is falsely small. The correct sample size for this design is 1 and the correct df is zero. The sample size and df are inflated for this design because the treatment was randomized to mouse and not to cell. Mouse is the experimental unit – the number of experimental units is what gives the degrees of freedom. The df are correct for inference about the two individuals (how compatible are the data and a model of sampling from the same individual?), but not for inference about the effect of genotype. We cannot infer anything about genotype with a sample size of 1, even with 20 measures per mouse, because any effect of treatment is completely confounded with other differences between the two mice.

16.4 Experimental designs in experimental bench biology

Given the basic principles above, let’s consider the kinds of experimental designs seen in experimental bench biology (Fig. ??).

Figure 16.1: Experimental designs in experimental bench biology. Images created with BioRender.com

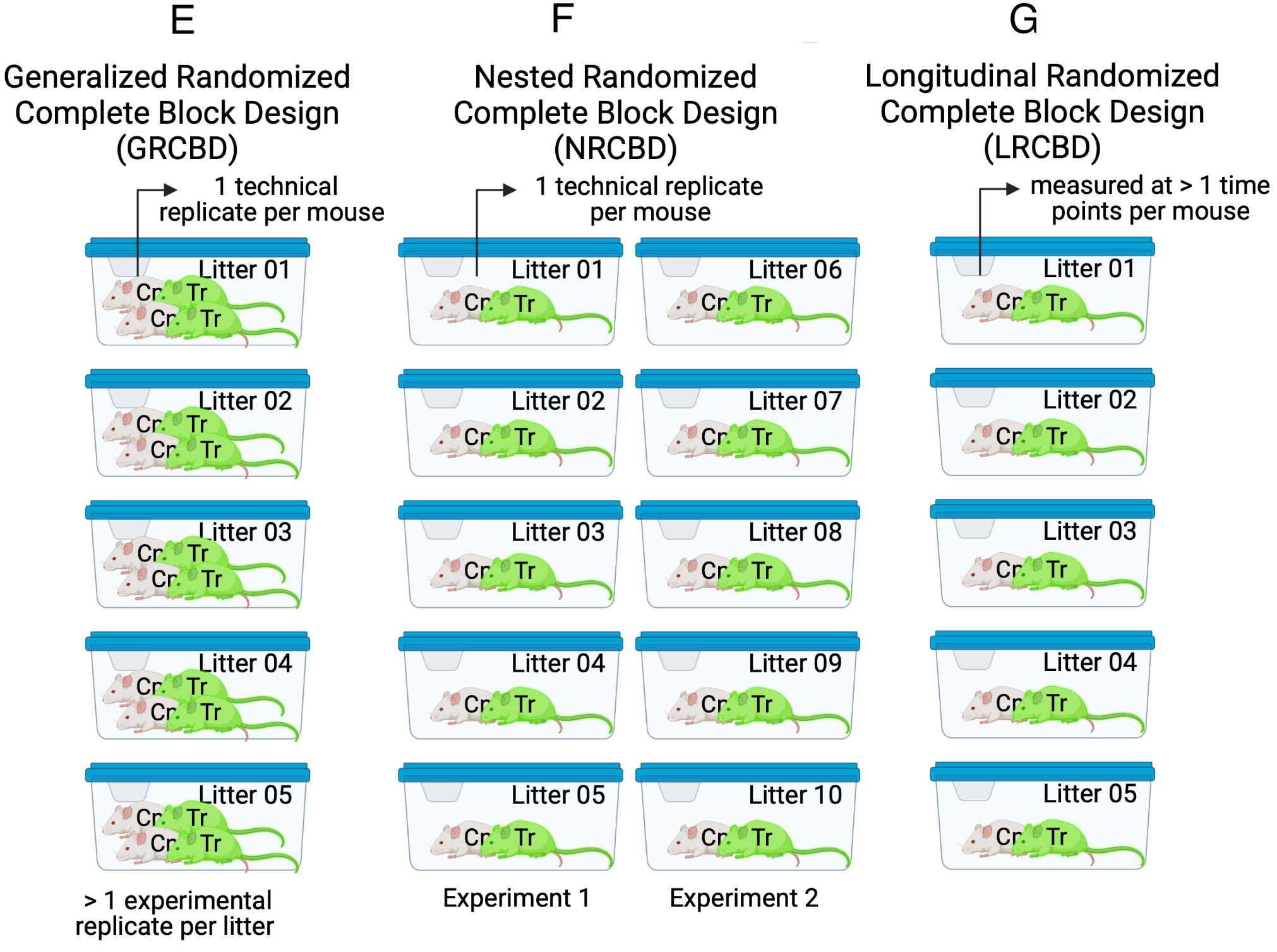
Figure 16.2: Experimental designs in experimental bench biology. Images created with BioRender.com

16.4.1 Notation for models

i = 1..t (treatments)

j = 1..b (blocks)

k = 1..r (experimental replications within a block or within a CRD with no block structure)

m = 1..s (subsamples or technical replicates)

16.4.2 Completely Randomized Design (CRD)

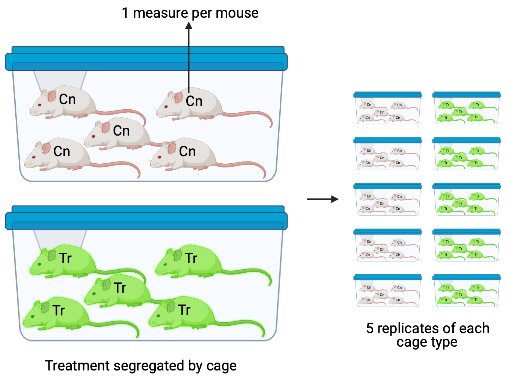
The Completely Randomized Design experiment in Figure ??A has a single factor, $\texttt{treatment}$ with two levels (“Cn” and “Tr”). Five mice are randomly assigned to each treatment level. Each mouse is bred from a different litter and housed in a separate cage. The researchers measure a single value of the response variable from each mouse. The five replicate mice per treatment are the treatment (biological) replicates. The design is completely randomized because there is no subgrouping due to batches. What kinds of subgrouping does this design avoid?

By using a single mouse per litter, there are no litter batches and subsets of mice don’t share litter effects – common litter responses to the Cn or Tr treatments. Each litter has a unique set of factors that contribute to the error variance of the measure of the response. Siblings from the same dam and sire share more genetic variation than non-siblings and this shared genetic variation contributes to phenotypes (including the response to treatment) that are more likely to be similar to each other than to non-siblings. Siblings from the same litter share the same history of maternal factors (maternal effects, including epigenetic effects) specific to the pregnancy and even the history of events leading up to the pregnancy. This shared non-genetic and epigenetic variation contributes to phenotypes (including the response to treatment) that are more likely to be similar to each other than to non-siblings. All response measures within a litter share the genetic, maternal environmental, and epigenetic components of the error variance unique to that litter and, as a consequence, the error (residuals) within a litter are more similar to each other than they are to the residuals between litters.

By housing each mouse in it’s own cage, there is no cage batch and subsets of mice don’t share cage effects – common cage responses to the Cn or Tr treatments. As stated earlier, each cage has a unique set of factors that contribute to the error variance of the measure of the response. Each cage shares a cage-specific history of temperature, humidity, food, light, interactions with animal facilities staff and behavioral interactions among the mice. All response measures within a cage share the component of the error variance unique to that cage and, as a consequence, the error (residuals) within a cage are more similar to each other than they are to the residuals between cages.

Examples:

Ten mice from separate litters are sampled. Five mice are randomly assigned to control. Five mice are randomly assigned to treatment. A single measure per mouse is taken. Mouse is the experimental unit. $t=2$, $b=0$, $r=5$, and $s=1$.
Ten cell cultures are created. Five cultures are randomly assigned to control and five to treatment. A single measure per culture is taken. Culture is the experimental unit. $t=2$, $b=0$, $r=5$, and $s=1$.

div style=“background-color:#cccccc; text-align:left; vertical-align: middle; padding:20px 47px;”> While most data from experiments in bench biology are analyzed as if the experimental design is a CRD, a good question is, what fraction of these actually are CRD? We know that many (most?) mouse experiments will have batched measures and correlated responses because most experiments are conducted with multiple mice per litter and/or cage (or equivalents in other model systems). Many cell culture data come from multiple replicates of the whole experiment – the experiment functions as a block. And time series experiments include multiple measures on the same experimental unit over time. Except for time series experiments, researchers in experimental bench biology are using almost exclusively statistical tests that assume independence of errors (the tests appropriate for CRDs). How this mismatch between experimental design and statistical practice affects the rate of false and true discovery in cell and molecular biology is entirely unknown.

16.4.3 Completely Randomized Design with Subsampling (CRDS) or “Nested Design”

The Completely Randomized Design with Subsampling experiment in Fig. ??B is exactly like the CRD except that the researchers measure multiple values of the response variable from each mouse under the same condition (that is, not different in treatment or time). The multiple measures are subsampled (technical) replicates.

Do not confuse subsampled replicates with measures of the response under different conditions in the same mouse, for example a measure from one brain slice under the control treatment and a measure from a second brain slice under the drug treatment. This example is a kind of Randomized Complete Block Design, which is outlined next and the core design in this chapter.
Do not confuse subsampled replicates with a measures of the response at different times in the same mouse, for example, the plasma glucose levels at baseline and at five post-baseline time points. This example is a kind of longitudinal design, which is outlined below and more thoroughly in the chapter Linear models for longitudinal experiments.
Do not confuse subsampled replicates with measures of different response variables from the same mouse, for example measures of the weights of five different skeletal muscles. This example is a kind of multiple response which is addressed xxx.

The technical replicates are a kind of pseudoreplication. The general linear model y ~ treatment fit to these data, including t-tests and traditional ANOVA, will have falsely high precision and falsely low p-values.

Examples:

Ten mice from separate litters are sampled. Five mice are randomly assigned to control. Five mice are randomly assigned to treatment. Multiple measures per mouse are taken. Example: five measures of Islet Area are measured in each pancreas. Mouse is the experimental unit. Each of the measures is a technical replicate because the treatment is not randomly assigned to each islet but to the whole mouse. $t=2$, $b=0$, $r=5$, and $s=5$.
Ten cell cultures are created. Five cultures are randomly assigned to control and five to treatment. Multiple measures per culture are taken. Example: Mitochondrial counts are measured from five cells in each culture. Culture is the experimental unit. Each of the counts is a technical replicate because the treatment is not randomly assigned to each cell but to the whole culture. $t=2$, $b=0$, $r=5$, and $s=5$.

Notes:

Subsampling can occur at multiple levels. Example: Ten mice from separate litters are sampled. Five mice are randomly assigned to control. Five mice are randomly assigned to treatment. Five neurons in a slice of brain tissue are identified in each mouse. From each neuron, the length of five dendrite spines are measured. The five measures of spine length are “nested within” neuron and the five neurons are “nested within” mouse. Nested subsampling can quickly lead to massive pseudoreplication and false discovery.

16.4.4 Randomized Complete Block Design (RCBD)

The Randomized Complete Block Design experiment in Figure ??C is similar to the CRD except that all treatment combinations (two here) are randomly assigned to sibling mice within a litter. Here, two mice from each litter are randomly selected and one is randomly assigned to “Cn” and the other to “Tr”. Each litter is randomly assigned to a unique cage. The researchers measure a single value of the response variable from each mouse. The five replicate mice per treatment are the treatment replicates. The litters (or cage) are the blocks. In this design, litter and cage effects are confounded but this has no consequence on the statistical model and inference unless the researchers want to explicitly estimate these effects separately. Compared to the CRD, this design requires fewer resources (five litters instead of ten, five cages instead of ten). Compared to the general linear model fit to data from the CRD (y ~ treatment), including t-tests and traditional ANOVA, the linear mixed model fit to the RCBD has increased precision and power. While many researchers seem to be designing experiments similar to this (“littermate controls”), most are failing to fit a statistical model that accounts for the batching and taking advantage of the increased precision and power.

Examples:

Ten mice are sampled. In each mouse, one forelimb is assigned to control and the other forelimb is assigned to treatment. Only a single measure on each side is taken. Limb is the experimental unit. Mouse is a block. $t=2$, $b=10$, $r=1$, and $s=1$.
Ten litters are sampled. In each litter, one sib is assigned to control and the other sib is assigned to treatment. Only a single measure on each sib is taken. Mouse is the experimental unit. Litter is a block. $t=2$, $b=10$, $r=1$, and $s=1$.
Two mice, each from a separate litter are sampled. One is randomly assigned to control and the other to treatment. Only a single measure of the response variable is taken per mouse. The experiment is replicated five times (five different days, each with a newly made set of reagents and machine calibrations). Mouse is the experimental unit. Experiment is a block. $t=2$, $b=5$, $r=1$, and $s=1$.

16.4.5 Randomized Split Plot Design (RSPD)

The Randomized Split Plot Design experiment in Figure ??D is similar to the RCBD except that there is now a second experimental factor that is crossed with the first experimental factor. An individual mouse acts as single experimental unit for one factor (here, $\texttt{genotype}$ with levels “WT” and “KO”) but acts as a block for the second experimental factor (here, $\texttt{treatment}$ with levels “Cn” and “Tr”). The first factor ($\texttt{genotype}$) is the main plot – the levels of the factor are randomly assigned to the main plots. The second factor ($\texttt{treatment}$) is the subplot – the levels of this factor are randomly assigned to the subplots. $\texttt{Litter}$ is a replicated block. Also in Figure ??D, a 2 x 2 RCBD with the same two experimental factors is shown for comparison. In the 2 x 2 RCBD, four mice per block (litter) are each randomly assigned one of the 2 x 2 combinations of $\texttt{genotype}$ and $\texttt{treatment}$).

16.4.6 Generalized Randomized Complete Block Design (GRCBD)

The Generalized Randomized Complete Block Design experiment in Figure ??E is similar to the RCBD except that two treatment replicates per block (litter/cage) are assigned.

Important and somewhat not intuitive Because the treatment replicates within a litter share common error variance, these do not act like independent replicates. One consequence of this is, the sample size ($n$) is five and not ten ($litters \times treatment replicates$). The general linear model y ~ treatment fit to these data, including t-tests and traditional ANOVA, will generally have falsely high precision and falsely low p-values.

16.4.7 Nested Randomized Complete Block Design (NRCBD)

The Nested Randomized Complete Block Design experiment in Figure ??F is similar to the RCBD except that there are now replicated experiments. This is a nested block design with litter (a block) nested within experiment (a block).

16.4.8 Longitudinal Randomized Complete Block Design (LRCBD)

The Longitudinal Randomized Complete Block Design experiment in Figure ??G is similar to the RCBD except that there are multiple measures of the response variable taken, each taken at a different time point, including baseline (time zero).

16.4.9 Variations due to multiple measures of the response variable

Similar to the CRDS above, the other basic designs can include subsampling, resulting in, for example, RCBDS or RSPDS. If there is subsampling within subsampled units, then we can designated these with “SS”, for example RCBDSS.

Similar to the LRCBD above, the other basic designs can include longitudinal sampling, resulting in, for example, LCRD or LRSPD.

16.5 Building the linear (mixed) model for clustered data

Notation

i = 1..t (treatments)
j = 1..b (blocks)
k = 1..r (experimental replications within a block)
m = 1..s (subsamples or technical replicates)

\[y_i = \beta_0 + \beta_i treatment_i + (\gamma_j block_j) + (\gamma_{ij} block_j treatment_i) + \varepsilon\]

16.6 Example 1 – A random intercepts and slopes explainer (demo1)

To introduce linear mixed models, I’m using data from Experiment 1g below. The design is $2 \times 2$ factorial with 4-5 mice per treatment combination. To simplify the explanation of random intercepts and random slopes in linear models with added random factors (linear mixed models), I flatten the analysis to a single treatment factor ($\texttt{treatment}$) with four levels (“Control”, “Tr1”, “Tr2”, “Tr3). The response is percent germinal centers ($\texttt{gc}$) in secondary lymphoid tissue. The experiment was replicated 4 times. Each replication is a batch. This batch information is in the variable $\texttt{experiment_id}$. Further detail isn’t necessary at this point.

Figure 16.3A is a response plot of the linear model lm(gc ~ treatment) fit to the whole data set, ignoring the fact that the data were collected in batches. This is the complete pooling fit. Figure 16.3B is a response plot of the linear model lm(gc ~ treatment) fit to the means of each treatment combination from each experiment. This is the means pooling fit.

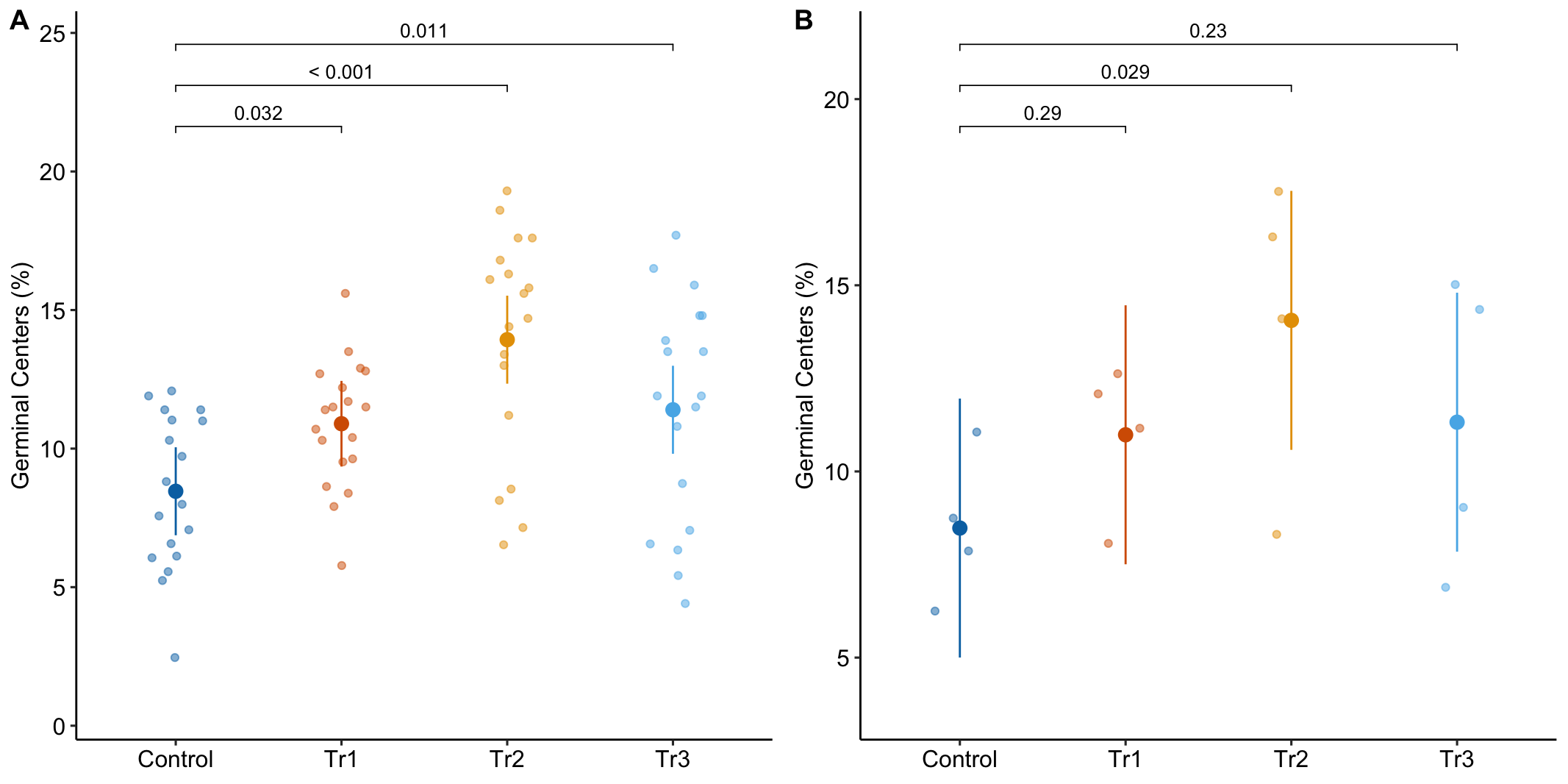
A. Response plot of the linear model gc ~ treatment fit to all exp1g data. B. Response plot of the linear model gc ~ treatment fit to the experiment means of the exp1g data.

Figure 16.3: A. Response plot of the linear model gc ~ treatment fit to all exp1g data. B. Response plot of the linear model gc ~ treatment fit to the experiment means of the exp1g data.

16.6.1 Batched measurements result in clustered residuals

Figure 16.4A is a plot of the residuals of the complete-pooling fit against $\texttt{experiment_id}$. The residuals are clustered by experiment. All residuals from experiment 1 are positive. All residuals from experiment 2 are negative. Residuals from experiment 3 are generally positive. Residuals from experiment 4 seem pretty random. This clustering by experiment is the same in the plot of the residuals of the means-pooling fit against $\texttt{experiment_id}$ (Figure 16.4B). The residuals are not independent in either fit. If you asked me to guess the sign of a residual and gave me the information that the measure was from experiment 1, I’d be correct 100% of the time. If the residuals were independent, I’d be correct, on average, 50% of the time. Independent residuals are randomly scattered about zero for within each experiment (Figure 16.4C).

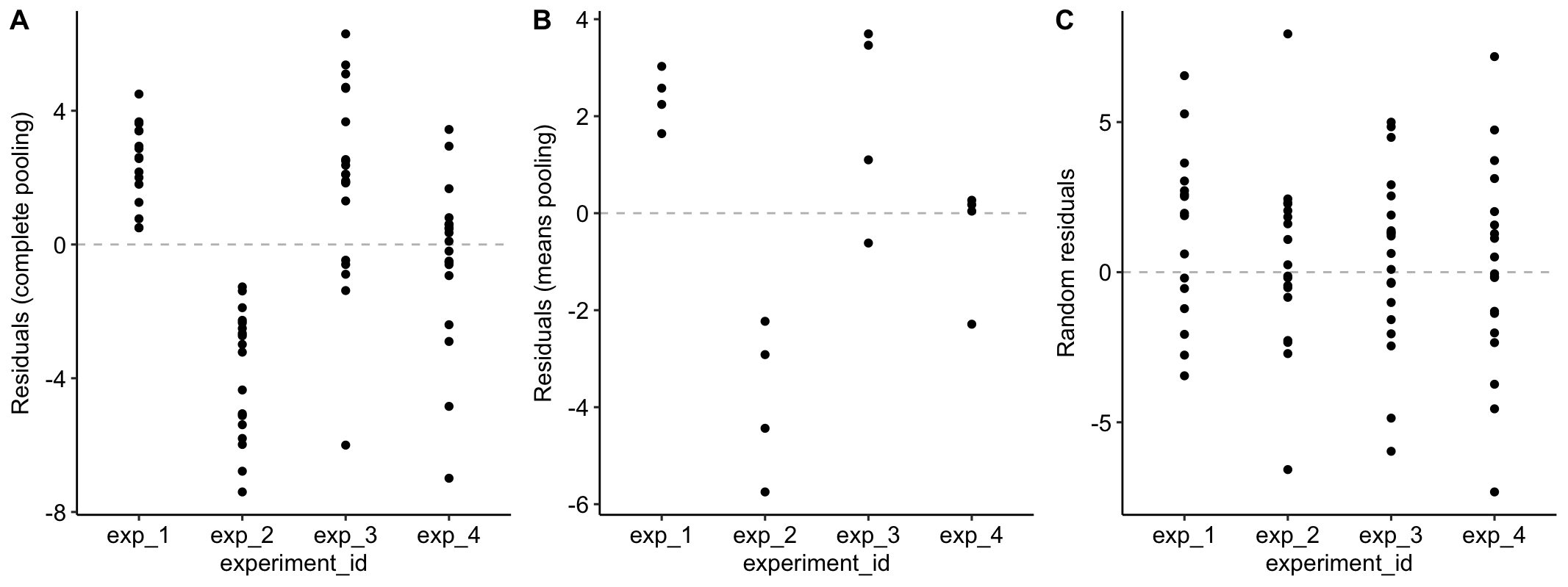
Figure 16.4: A. Residuals of the model fit to all demo1 data. B. Residuals of the model fit to the mean demo1 data.

16.6.2 Clustered residuals result in correlated error

An assumption of inference from a linear model is independence – each response is independently drawn from a distribution of random values. In Experiment 1g, the experiments are batches and the batched data results in correlated error unless modeled. One way to see this correlated error is to use the residuals from the means-pooled fit.

aggregate the data by computing the means for each treatment level within each experiment.
fit the fixed effect model (the model without added random factors) to the aggregated data
compute the residuals from the model
cast (or spread) the residuals for each treatment into its own column. This creates a 4 rows (experiment) $\times$ 4 columns (treatments) matrix of residuals.
Compute the correlations among the four treatment combination columns. This is the correlated error due to the batch effect of $\texttt{experiment_id}$.

Table 16.1: Residuals of fixed affect model fit to aggregated data. The residuals are split into each treatment.
experiment_id	Control	Tr1	Tr2	Tr3
exp_1	2.578125	1.64075	2.2425	3.027125
exp_2	-2.229375	-2.91625	-5.7475	-4.435375
exp_3	-0.615375	1.09975	3.4625	3.697125
exp_4	0.266625	0.17575	0.0425	-2.288875

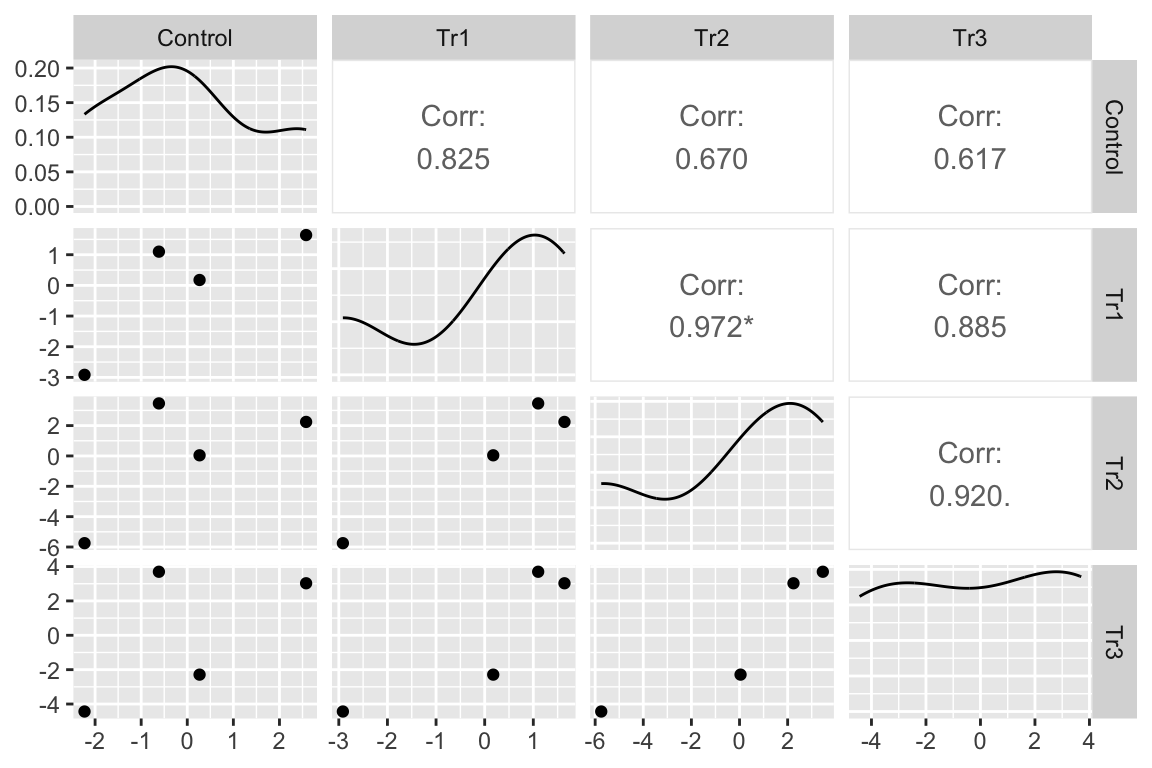
I’ve used GGally::ggpairs to compute and display the correlations as a matrix. The lower triangle of matrix elements contains the scatterplot of the residuals for the treatment combination defined by the row and column headers. The upper triangle of elements contains the Pearson correlation. With only four experiment residuals per treatment combination, large correlations will be common. But all correlations are large, positive values. The asterisks indicate values that would be an unexpected surprise under a null model of no correlation.

We could explicitly model correlated error with a linear model for correlated error using the nlme::gls function, using a model for the correlated error that matches our knowledge of how the data were generated (from experiment batches). In this chapter, we implicitly model the correlated error using a linear model with added random factors – a linear mixed model. What we explicitly model in a linear mixed model is hierarchical levels of variance.

16.6.3 In blocked designs, clustered residuals adds a variance component that masks treatment effects

The variance among the experiments within a treatment is much greater than the variance among the treatment means. A consequence of this is, the experiment effect masks the effect of treatment. We can manually unmask this by

compute the experiment means across all treatment combinations.
create a gc variable without variation among experiment means (“adjusted for experiment_id”).

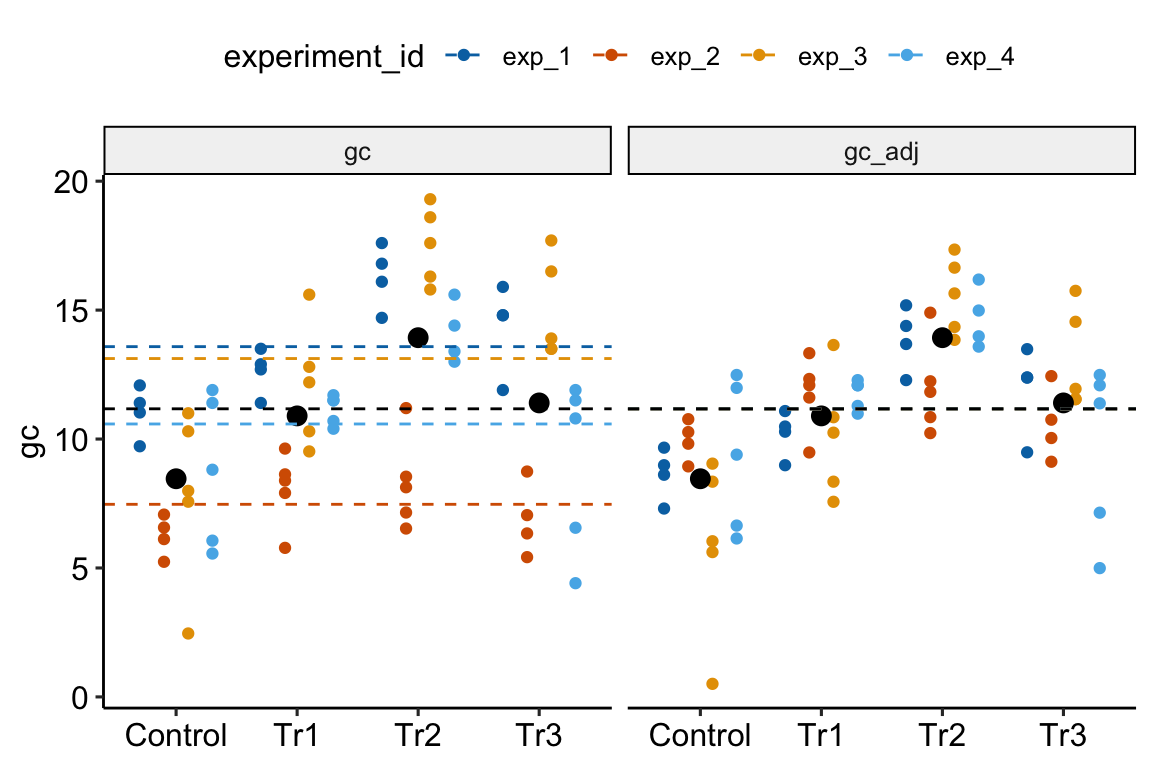
Adjusting for variance among experiments. The black, dashed line is the grand-mean response. In the left panel, the colored, dashed lines are the mean gc for each experiment, ignoring treatment. In the right panel, the individual values have been shifted (adjusted) by centering the experiment means. This has the effect of reducing the error variance -- the spread of the values around the treatment means (large black dots).

Figure 16.5: Adjusting for variance among experiments. The black, dashed line is the grand-mean response. In the left panel, the colored, dashed lines are the mean gc for each experiment, ignoring treatment. In the right panel, the individual values have been shifted (adjusted) by centering the experiment means. This has the effect of reducing the error variance – the spread of the values around the treatment means (large black dots).

In Figure 16.5, the black dots are the modeled means of each treatment combination. The small colored dots are the measured values of the response for each $\texttt{experiment_id}$ in the left panel and the experiment-adjusted values in the right panel. The black, dashed line is the grand-mean response. The colored, dashed lines are the means of all responses in each experiment. These means are equal in the right panel (and covered by the black line) because the variation among the means has been adjusted away. What is left is error variation uncontaminated by $\texttt{experiment_id}$.

In Experiment 1g, $\texttt{experiment_id}$ is a nuissance variable – it adds to the noise. In the exercise above, the effects of the treatment variables are adjusted for the elevation of batch effects on the overal batch mean. Linear mixed models are more sophisticated than this. In a linear mixed model, the effects of the treatment variables are adjusted for the elevations of batch effects on the intercept and batch effects on the slopes (or some combination of these). These are the random intercepts and random slopes.

16.6.4 Linear mixed models are linear models with added random factors

A linear model adds some combination of random intercepts and random slopes to a linear model.

\[ \begin{equation} \texttt{gc}_{jk} = (\beta_{0} + \gamma_{0j}) + (\beta_{k} + \gamma_{kj}) \texttt{treatment}_{k} + \varepsilon \tag{16.1} \end{equation} \]

A random intercept for experiment j is the sum of the fixed intercept ($\beta_0$) and a random intercept effect ($\gamma_{0j}$). I’ve embedded these within parentheses to show how these combine into the random intercept. A random slope for batch j is the sum of the fixed slope ($\beta_k$) for the non-reference level $k$ and a random slope effect ($\gamma_{kj}$). I’ve embedded these within parentheses to show how these combine into the random slopes.

There is a different $\gamma_{0j}$ for each experiment. There is a different $\gamma_{kj}$ for each combination of non-reference level and experiment. The $\gamma_0j$ and $\gamma_kj$ are modeled as if the values for each experiment is a random draw from an infinite number of experiments. This is why $\gamma_{0j}$ and $\gamma_{kj}$ are random effects. In contrast, $\beta_0$ and the three $\beta_k$ for the non-reference treatment levels are the same for all experiments – this is why $\beta_0$ is known as fixed effects (technically, $\beta_0$ is a mean and not an effect).

Model (16.1) is fit to the Example 1 data using lme4::lmer()

demo1_m1 <- lmer(gc ~ treatment +
                   (treatment | experiment_id),
                 data = demo1)

Notes

(treatment | experiment_id) specifies a random intercept for all levels of $\texttt{experiment_id}$ and a random slope for all combinations the levels of $\texttt{experiment_id}$ and the non-reference levels of $\texttt{treatment}$

16.6.5 What the random effects are

Random intercepts model batch effects in the reference treatment level. 16.6A illustrates random intercepts and random intercept effects. The large, colored dots are the modeled means of each experiment for each treatment combination. For the reference treatment level (“Control”), each mean is the sum of the estimated fixed intercept ($b_0$), shown by the dashed gray line, and the estimated random intercept effect ($g_{0j}$) for experiment j. The random intercept effects are the vertical, colored lines.

Random slopes model the effect of treatment on batch effects in the non-reference treatment levels. 16.6B illustrates random slopes and random slope effects, focusing on the slopes for the 2nd non-reference treatment level (“Tr2”). The angled black line is the estimated fixed slope $b_2$ for this level. The colored lines are the random slopes for each experiment. The pale, gray dots are where the modeled means at the Tr2 level would be if there were no random slope effect – as if we took the large colored dots at “Control” and rigidly shifted them up the black line to “Tr2”. The estimated random slope effects $\mathrm{g}_{2j}$ are the difference between these large, gray dots and the modeled means.

$What random intercepts and slopes are. (A) A random intercept for batch $j$ is the difference between the fixed intercept and the modeled mean for batch $j$ in the reference treatment level. The random intercepts for experiments 1 ($\mathrm{g}_{0.1}$) and 2 ($\mathrm{g}_{0.2}$) are shown with brackets. (B) The fixed slope for the "Tr2" is illustrated with a bracket. The large, grey dots are the expected values for each batch (experiment_id) in the "Tr2" treatment if the random slope effects are zero. A random slope for batch $j$ is the difference between the expected value for batch j and the modeled mean for batch $j$. The random slope for experiment 2 in "Tr2" ($\mathrm{g}_{2.2}$) is shown with a bracket.$

Figure 16.6: What random intercepts and slopes are. (A) A random intercept for batch $j$ is the difference between the fixed intercept and the modeled mean for batch $j$ in the reference treatment level. The random intercepts for experiments 1 ($\mathrm{g}_{0.1}$) and 2 ($\mathrm{g}_{0.2}$) are shown with brackets. (B) The fixed slope for the “Tr2” is illustrated with a bracket. The large, grey dots are the expected values for each batch (experiment_id) in the “Tr2” treatment if the random slope effects are zero. A random slope for batch $j$ is the difference between the expected value for batch j and the modeled mean for batch $j$. The random slope for experiment 2 in “Tr2” ($\mathrm{g}_{2.2}$) is shown with a bracket.

16.6.6 In a blocked design, a linear model with added random effects increases precision of treatment effects

\[ \begin{equation} \texttt{gc}_{jk} = \beta_{0} + \beta_{k} \texttt{treatment}_{k} + (\gamma_{0j} + \gamma_{kj}\texttt{treatment}_{k} + \varepsilon) \tag{16.2} \end{equation} \]

If the random intercepts and random slopes aren’t modeled, this among-experiment variance is shifted to the error variance because the intercept effects and slope effects aren’t estimated but absorbed by the error – everything in Model (16.2) will be estimated by the residuals. As a consequence, the estimate of $\sigma$ (the square root of the error variance) for the linear mixed model is smaller than that for the linear model with only fixed effects.

# sigma for the lmm
m1 <- lmer(gc ~ treatment +
                   (treatment | experiment_id),
                 data = demo1)
summary(m1)$sigma

## [1] 1.931339

# sigma for the fixed lm
m2 <- lm(gc ~ treatment,
                 data = demo1)
summary(m2)$sigma

## [1] 3.376402

The consequence of the smaller estimate of $\sigma$ in the linear mixed model on inference (confidence intervals and p-values) depends on the number of subsamples, the variance of the random effects relative to the variance of the residual error, and the correlation among the random effects.

16.6.7 The correlation among random intercepts and slopes

Again, here is the linear mixed model fit to the experiment 1g data.

\[ \begin{equation} \texttt{gc}_{jk} = (\beta_{0} + \gamma_{0j}) + (\beta_{k} + \gamma_{kj}) \texttt{treatment}_{k} + \varepsilon \end{equation} \]

Think about how this model generates data. We have four experiments, so we randomly draw four $\gamma_{0j}$ from a normal distribution with some variance $\sigma_{0}^2$. And, for each non-reference treatment, we randomly draw four $\gamma_{0k}$ from a normal distribution with some variance $\sigma_{k}^2$. This gives us a matrix of four columns (one random intercept and three random slopes) and four rows (four experiments).

intercept	slope 1	slope 2	slope 3
$\gamma_{0.1}$	$\gamma_{1.1}$	$\gamma_{2.1}$	$\gamma_{3.1}$
$\gamma_{0.2}$	$\gamma_{1.2}$	$\gamma_{2.2}$	$\gamma_{3.2}$
$\gamma_{0.3}$	$\gamma_{1.3}$	$\gamma_{2.3}$	$\gamma_{3.3}$
$\gamma_{0.4}$	$\gamma_{1.4}$	$\gamma_{2.4}$	$\gamma_{3.4}$

To randomly sample these values, the model needs not only the variances ($\sigma_k^2$) for each column (random effect) but also a correlation for each pair of columns. These correlations are the off-diagonal elements of the correlation matrix of random effects.

1	COR($\gamma_{0}$, $\gamma_{1}$)	COR($\gamma_{0}$, $\gamma_{2}$)	COR($\gamma_{0}$, $\gamma_{3}$)
COR($\gamma_{1}$, $\gamma_{0}$)	1	COR($\gamma_{1}$, $\gamma_{2}$)	COR($\gamma_{1}$, $\gamma_{3}$)
COR($\gamma_{2}$, $\gamma_{0}$)	COR($\gamma_{2}$, $\gamma_{1}$)	1	COR($\gamma_{2}$, $\gamma_{3}$)
COR($\gamma_{3}$, $\gamma_{0}$)	COR($\gamma_{3}$, $\gamma_{1}$)	COR($\gamma_{3}$, $\gamma_{2}$)	1

In the models fit in this text, a researcher doesn’t specify these variances and correlations. Instead, these are parameters estimated by the model. Here is a summary of the estimates of the variances of the random effects and of the correlations among the random effects for the linear mixed model fit to the experiment 1g data.

##  Groups        Name         Std.Dev. Corr                
##  experiment_id (Intercept)  1.7710                       
##                treatmentTr1 0.9642   -0.025              
##                treatmentTr2 2.9026    0.458  0.876       
##                treatmentTr3 2.9910    0.300  0.879  0.938
##  Residual                   1.9313

The first four values in the column “Std.Dev.” are the square roots of the estimated variances for the random effects given in the column “Name”. The last value in column “Std.Dev.” is the square roots of the estimate of $\sigma^2$ (the error variance). The (lower) triangular matrix of values under “Corr” are the estimates of the correlations among the random effects. The variance of the random effects and the correlation among the random effects creates the correlated error described above but do not confuse these different correlations (this is easy to confuse, you are not alone).

A compact way to view these variances and correlations is a matrix with the random effect standard deviations on the diagonal and the correlations on the off-diagonal. I’ll refer to this as the VarCorr matrix after the lme4 function used to get the values.

Table 16.2: The Varcorr matrix. Standard deviations of random effects on the diagonal. Correlations of random effects on the off-diagonal.

(Intercept)	1.77
treatmentTr1	-0.03	0.96
treatmentTr2	0.46	0.88	2.90
treatmentTr3	0.30	0.88	0.94	2.99

It’s probably not worth trying to understand the experimental reason underneath the correlations among the random effects. But, researchers might want to sleuth out why a lab is getting high random intercept and slope variances, relative to the error variances, as these could indicate potential sources of improvement in lab protocols.

16.6.8 Clustered residuals create heterogeneity among treatments

The variances of the four treatments are

treatment	Var
Control	7.8
Tr1	5.2
Tr2	16.2
Tr3	16.7

In chapter xxx, I stated that heterogeneity of variances can arise because of clustered data. Why does clustered data generate heterogeneity? Let’s keep peeking at the linear mixed model fit to the experiment 1g data.

\[ \begin{equation} \texttt{gc}_{jk} = (\beta_{0} + \gamma_{0j}) + (\beta_{k} + \gamma_{kj}) \texttt{treatment}_{k} + \varepsilon \end{equation} \]

In a linear model with fixed effects only, the expected variance for any treatment for any treatment is $\sigma^2$. But if the data are batched, the expected variances include components due to the batch and these batch components depend on the treatment. This creates heterogeneity.

To understand this, first some rules of expected variance. The random variable $\texttt{C}$ is the sum of two random variables $\texttt{A}$ and $\texttt{B}$. The variances of these variables are $\sigma_{C}^2$, $\sigma_{A}^2$, and $\sigma_{B}^2$.

The expected variance of $\texttt{C}$ if $\texttt{A}$ and $\texttt{B}$ are independent (uncorrelated) is $\sigma_{C}^2 = \sigma_{A}^2 + \sigma_{B}^2$ (this equation should look familiar).
The expected variance of $\texttt{C}$ if $\texttt{A}$ and $\texttt{B}$ are not independent (correlated) is $\sigma_{C}^2 = \sigma_{A}^2 + \sigma_{B}^2 + 2\sigma_{A}\ \sigma_{B}\ \rho_{A,B}$ where $\rho_{A,B}$ is the expected correlation between $\texttt{A}$ and $\texttt{B}$ (this equation might also look familiar).

Here is some code to better know expected variances of the sum of two correlated random variables.

# copy, paste, and explore
n <- 10^4
rho <- 0.6 # change this to any value between -1 and 1
b <- sqrt(abs(rho))
z <- rnorm(n)
A <- b*z + sqrt(1-b^2)*rnorm(n)
B <- sign(rho)*b*z + sqrt(1-b^2)*rnorm(n)
cor(A,B) # should be close to rho
C <- A + B
sd(A)^2 # should be close to 1
sd(B)^2 # should be close to 1
sd(C)^2 # should be close to 1^2 + 1^2 + 2*1*1*rho
sd(A)^2 + sd(B)^2 + 2*sd(A)*sd(B)*cor(A,B) # should equal previous line

Using these rules and the standard deviations of the random effects given above we can compute the expected variances of the treatment groups given the fit model.

For the variance of the reference (“Control”) group, we need to add to $\sigma^2$ the variance of the random intercept using rule #1 (the residuals are not correlated with random intercepts or slopes). The modeled variance is a less than the actual variance of the Control group.

summary(m1)$sigma^2 + 1.7710^2

## [1] 6.866512

For the variance of a non-reference group, we need to add to $\sigma^2$ the variance of the random intercept and the variance of the random slope for the treatment and the component due to the correlation between the random slope for the treatment and the random intercept. For Tr2, this is

# error + intercept + slope + cor(intercept, slope)
(summary(m1)$sigma^2) + (1.7710^2) + (2.9026^2) + (2 * 1.7710 * 2.9026 * 0.458)

## [1] 20.0003

which is a bit higher than the measured variance.

16.6.9 Linear mixed models are flexible

One more look at the linear mixed model fit to the experiment 1g data.

\[ \begin{equation} \texttt{gc}_{jk} = (\beta_{0} + \gamma_{0j}) + (\beta_{k} + \gamma_{kj}) \texttt{treatment}_{k} + \varepsilon \end{equation} \]

The linear mixed model specifies both a random intercept and a random slope but a researcher might limit the model to the random intercept only, or less commonly, the random slope only. Or a researcher might replace the random slope with a second random intercept that captures variance in the batch by treatment combinations like a random slope. Or a researcher might model the structure (correlated error and heterogeneity of variances) in the residuals in addition to adding random factors to the model.

16.6.10 A random intercept only model

demo1_m2 <- lmer(gc ~ treatment +
                   (1 | experiment_id),
                 data = demo1)

Notes

Model demo1_m2 specifies only a random intercept for each of the levels of $\texttt{experiment_id}$. The exclusion of the random slopes ia a kind of model simplification.
In experiments without subsampling, random slopes cannot be added to the model because there is no variation with a treatment by batch combination.
In experiments with subsampling, a researcher might exclude a random slope term for several reasons, including

it is the culture in many subfields to only include a random intercept (no, this is not a good reason)
the computation of the model fit returned a convergence warning
model comparison suggested that a model with the random slope was too complex given the data. A useful statistic for comparing models with different random effects specifications is the AIC, which is introduced in Section 16.6.12 below.

16.6.11 A model including an interaction intercept

demo1_m3 <- lmer(gc ~ treatment +
                   (1 | experiment_id) +
                   (1 | experiment_id:treatment),
                 data = demo1)

Notes

(1 | experiment_id:treatment) models a random intercept for all combinations of the levels of $\texttt{experiment_id}$ and $\texttt{treatment}$. This interaction intercept is an alternative to a random slope for modeling treatment-specific batch effects.

16.6.12 AIC and model selection – which model to report?

Three different linear mixed models were fit to the Example 1 data: demo1_m1, demo1_m2, and demo1_m3. Which model do we report? A useful stastistic for this decision is a statistic known as the AIC.

Table 16.3: AIC of the two alternative models fit to Example 1 data
Model	AIC
demo1_m1	344.1529
demo1_m2	344.0765
demo1_m3	337.5332

Notes

AIC (Akaike Information Criterion) is a relative measure of model quality. Compare this to $R^2$, which is an absolute measure of goodness of fit. The AIC formula has two parts, one is a kind of goodness of fit (like $R^2$) and the other is a penalty based on the number of parameters in the model. As the goodness of fit increases, the AIC goes down. As the number of parameters increases, the AIC goes up. The model with the lowest AIC is the highest quality model. The actual value of AIC, unlike $R^2$, does not have any absolute meaning; it is only meaningful relative to the AICs computed from fits to different models to the same data.
The AIC of the three models suggests that we report Model demo1_m3.

16.6.13 The specification of random effects matters

Inference will often be very different between these two models as they make very different

Table 16.4: Contrasts from the three linear mixed models fit to the Example 1 data.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
intercepts + slopes (m1)
Tr1 - Control	2.54	0.804	2.978	-0.03	5.11	3.16	0.05150
Tr2 - Control	5.61	1.591	2.997	0.54	10.67	3.52	0.03885
Tr3 - Control	2.85	1.631	2.997	-2.35	8.04	1.74	0.17949
intercepts only (m2)
Tr1 - Control	2.64	0.755	66.005	1.13	4.15	3.49	0.00086
Tr2 - Control	5.65	0.766	66.014	4.12	7.18	7.38	0.00000
Tr3 - Control	2.94	0.765	66.000	1.41	4.47	3.85	0.00027
intercept + interaction intercept (m3)
Tr1 - Control	2.54	1.214	8.912	-0.21	5.29	2.09	0.06616
Tr2 - Control	5.60	1.219	9.061	2.84	8.35	4.59	0.00128
Tr3 - Control	2.87	1.219	9.052	0.12	5.63	2.36	0.04269

Notes

Inference from the intercept only model (demo1_m2) is almost certainly too optimistic based on simulations that show that intercept only models can be highly anti-conservative (too narrow confidence intervals and too small p-values).
Humans have evolved to make up rational explanations – do not convince yourself that the model with the smallest p-values is the scientifically most rational model.

16.6.14 Mixed Effect and Repeated Measures ANOVA

Two-way mixed-effect ANOVA (some fields would call this a repeated measures ANOVA) is equivalent to Model demo1_m3 in this case. More generally, the two are equal in balanced designs – the same number of subsamples in all treatment x batch combinations.

demo1_m4 <- aov_4(gc ~ treatment + 
                   (treatment | experiment_id),
                 data = demo1)

Notes 1. The function afex::aov4 is used for specifying ANOVA models that are special cases of linear mixed models. 2. The model formula in Model demo1_m2 looks exactly like that the random intercepts and slopes model (Model demo1_m1) but these are not the same. 3. One can use either a univariate or multivariate model for mixed or repeated measures ANOVA – see section 16.7.11.

Table 16.5: Contrasts from the two-way mixed effect ANOVA model demo1_m4.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
Tr1 - Control	2.50	0.599	3	0.60	4.41	4.18	0.02488
Tr2 - Control	5.58	1.559	3	0.62	10.54	3.58	0.03734
Tr3 - Control	2.84	1.586	3	-2.20	7.89	1.79	0.17095

16.6.15 Pseudoreplication

16.7 Example 2 – experiments without subsampling replication (exp6g)

This example introduces linear mixed models for batches that contain all treatment levels of a single factor but no subsampling replication. In this example, the batch is the individual mouse ($\texttt{mouse_id}$). There are four measures of the response variable on each mouse, one measure per treatment level. When there is no subsampling replication, we cannot add a random slope to the model because there is only a single observation at each treatment level and a slope would fit the point at the reference level and the point at the non-reference level perfectly. However, we can explicitly model variation in the correlated error and heterogeneity in the variances among treatments as an alternative to modeling a random slope.

Reversing a model of Parkinson’s disease with in situ converted nigral neurons

Public source

Source figure: Fig. 6g

Source data: Source Data Fig. 6

16.7.1 Understand the data

In this study, the researchers investigated the effectiveness of knocking down the protein PTBP1 to induce astrocytes to convert to neurons in a motor processing region of the brain. Experimental lesions of this region of the brain is a model of Parkinson’s disease. In Experiment 6g, the researchers

Generated a lesion in the motor processing region using 6-hydroxydopamine (6-OHDA). The lesion disrupts the ability to control the contralateral (opposite side) forelimb.
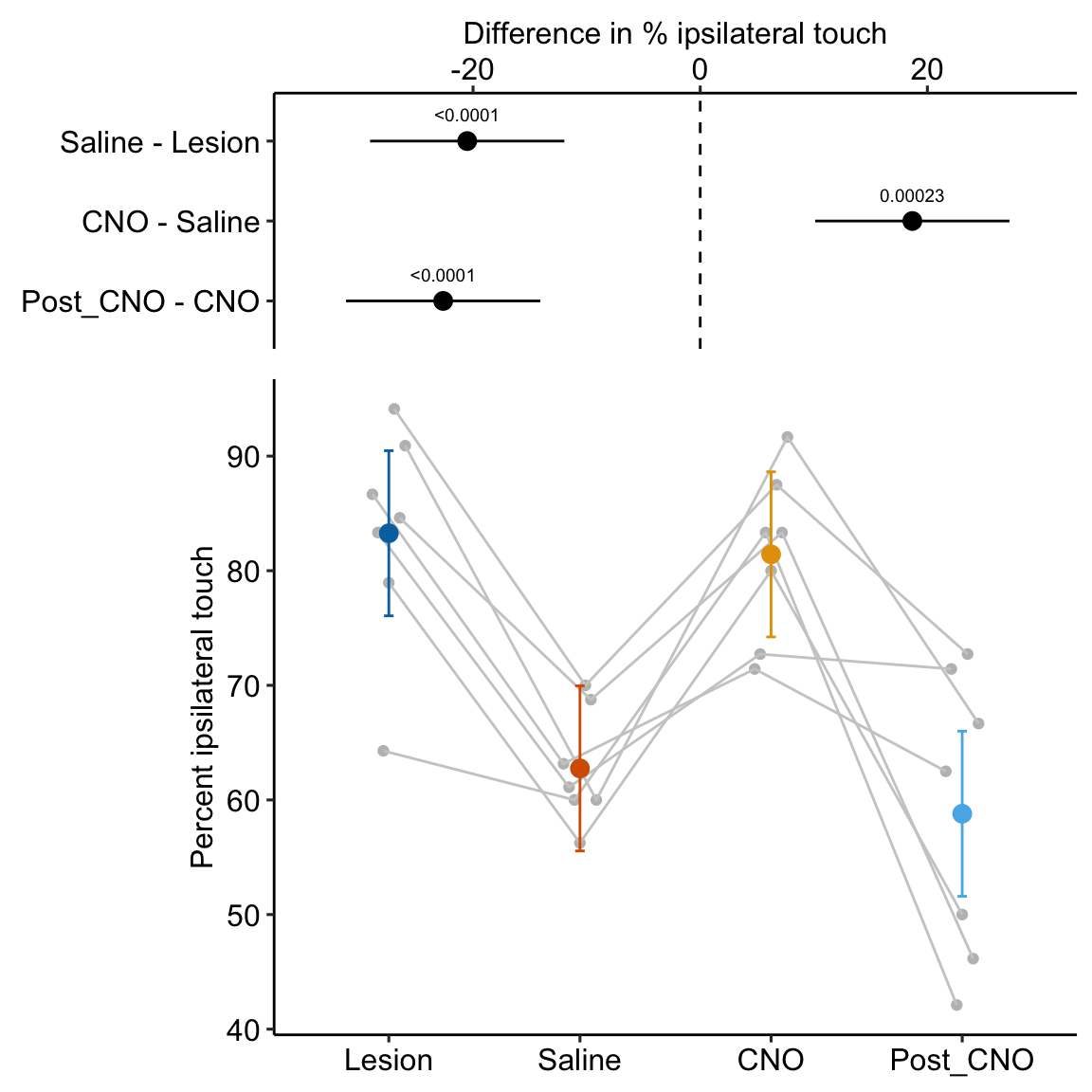
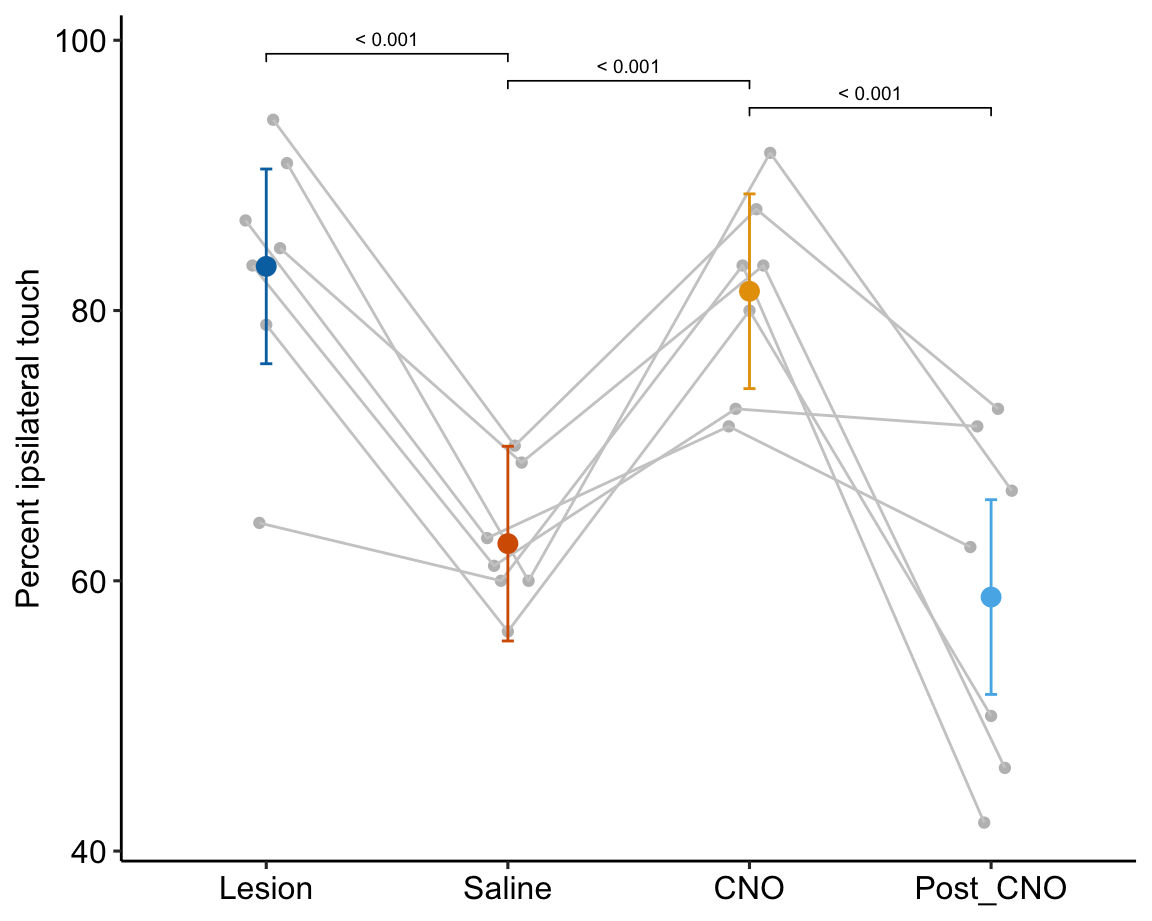
One month after the lesion, measured the percent of ipsilateral (same side) forepaw touches (the forelimb extending out and touching the surface) in a test of exploration in a new environment (the “cylinder test”). The expected percent in an intact mouse is 50%. In a lesioned mouse, the percent should be much greater than 50% since there is less control of the contralateral limb. The measure at this point is in the treatment “Lesion”. This is the positive control.
Converted astrocytes in the lesion to functional neurons by knocking down PTBP1.
Two months after knockdown, gave the mouse saline and remeasured percent ipsilateral touches in a cylinder test. If the knockdown worked as expected, there should be closer to 50% ipsilateral touches. The measure at this point is in the treatment “Saline”. The comparison with Lesion is a focal test.
Inhibited neuron action in the converted neurons using clozapine-N-oxide (CNO), which suppresses neuron electrical activity. Then, remeasured percent ipsilateral touches in a cylinder test. If the CNO worked as expected, there should be much greater than 50% ipsilateral touches since there should be re-loss of control of the contralateral limb. The measure at this point is in the treatment “CNO”. The comparison with Saline is a focal test.
Allowed three days for the CNO to degrade, then, remeasured percent ipsilateral touches in a cylinder test. If the CNO degraded as expected, the converted neurons should be functional and there should be closer to 50% ipsilateral touches. The measure at this point is in the treatment “Post_CNO”. The comparison with CNO is a focal test.

The design is $4 \times 1$ – a single treatment with four levels (“Lesion”, “Saline”, “CNO”, “Post_CNO”)

The planned contrasts are

Saline - Lesion. This measures the effect of the knockdown and conversion of astrocytes to functional neurons.
CNO - Saline. This measures the effect of inhibiting the converted neurons to test if it was these and not some other neurons that account for the effect in contrast 1.
Post_CNO - CNO. This is probing the same expectation as contrast 2.

16.7.2 Model fit and inference

16.7.2.1 Fit the model

exp6g_m1a <- lmer(touch ~ treatment + (1|mouse_id), data = exp6g)

# alt model
exp6g_m1b <- lme(touch ~ treatment,
                random = ~1|mouse_id,
                correlation = corSymm(form = ~ 1 | mouse_id),
                weights = varIdent(form = ~ 1 | treatment),
                data = exp6g)

AIC(exp6g_m1a, exp6g_m1b)

##           df      AIC
## exp6g_m1a  6 191.3367
## exp6g_m1b 15 198.3888

# report model a
exp6g_m1 <- exp6g_m1a

exp6g_m1b overparameterizes, report exp6g_m1a (see Alternative models for exp6g below)

16.7.2.2 Inference from the model

exp6g_m1_coef <- cbind(coef(summary(exp6g_m1)),
                       confint(exp6g_m1)[-c(1:2),])

# exp5c_m1_coef %>%
#   kable(digits = c(2,3,1,1,4,2,2)) %>%
#   kable_styling()

exp6g_m1_emm <- emmeans(exp6g_m1, specs = c("treatment"))

treatment	emmean	SE	df	lower.CL	upper.CL
Lesion	83.3	3.44	18.9	76.1	90.47
Saline	62.8	3.44	18.9	55.5	69.96
CNO	81.4	3.44	18.9	74.2	88.63
Post_CNO	58.8	3.44	18.9	51.6	66.00

# exp6g_m1_emm # print in console to get row numbers
# set the mean as the row number from the emmeans table
lesion <- c(1,0,0,0)
saline <- c(0,1,0,0)
cno <- c(0,0,1,0)
post_cno <- c(0,0,0,1)

exp6g_m1_planned <- contrast(exp6g_m1_emm,
                       method = list(
                         "Saline - Lesion" = c(saline - lesion),
                         "CNO - Saline" = c(cno - saline),
                         "Post_CNO - CNO" = c(post_cno - cno)
                       ),
                       adjust = "none"
) %>%
  summary(infer = TRUE)

contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
Saline - Lesion	-20.52	4.071	18	-29.07	-11.96	-5.04	0.00009
CNO - Saline	18.67	4.071	18	10.12	27.23	4.59	0.00023
Post_CNO - CNO	-22.63	4.071	18	-31.18	-14.08	-5.56	0.00003

16.7.2.3 Plot the model

Figure 16.7: Treatment effect on ipsilateral touch, as percent of all touches. Gray dots connected by lines are individual mice.

16.7.2.4 Alternaplot the model

Figure 16.8: Ipsilateral touch (percent of all touches) response to different treatments. Gray dots connected by lines are individual mice.

16.7.3 The model exp6g_m1 adds a random intercept but not a random slope

The model fit to the exp6g data is

\[ \begin{equation} \texttt{touch}_{jk} = (\beta_{0} + \gamma_{0j}) + (\beta_{k} + \gamma_{jk}) \texttt{treatment}_{k} + \varepsilon \end{equation} \]

Notes

Again, in experiments without subsampling, we cannot add a random slope to the model (for each mouse, there is a single observation at each treatment level so a slope would fit the two points perfectly).

16.7.4 The fixed effect coefficients of model exp6g_m1

The fixed effect coefficients of model exp6g_m1 are

	Estimate	Std. Error	df	t value	Pr(>\|t\|)	2.5 %	97.5 %
(Intercept)	83.27	3.441	18.9	24.20	0.0000	76.72	89.81
treatmentSaline	-20.52	4.071	18.0	-5.04	0.0001	-28.25	-12.78
treatmentCNO	-1.84	4.071	18.0	-0.45	0.6565	-9.58	5.90
treatmentPost_CNO	-24.47	4.071	18.0	-6.01	0.0000	-32.21	-16.73

Notes

The interpretation of the fixed effectcs coefficients have the usual interpretation (see The coefficients of a linear model using dummy coding have a useful interpretation). Figure 16.9 is a reminder.

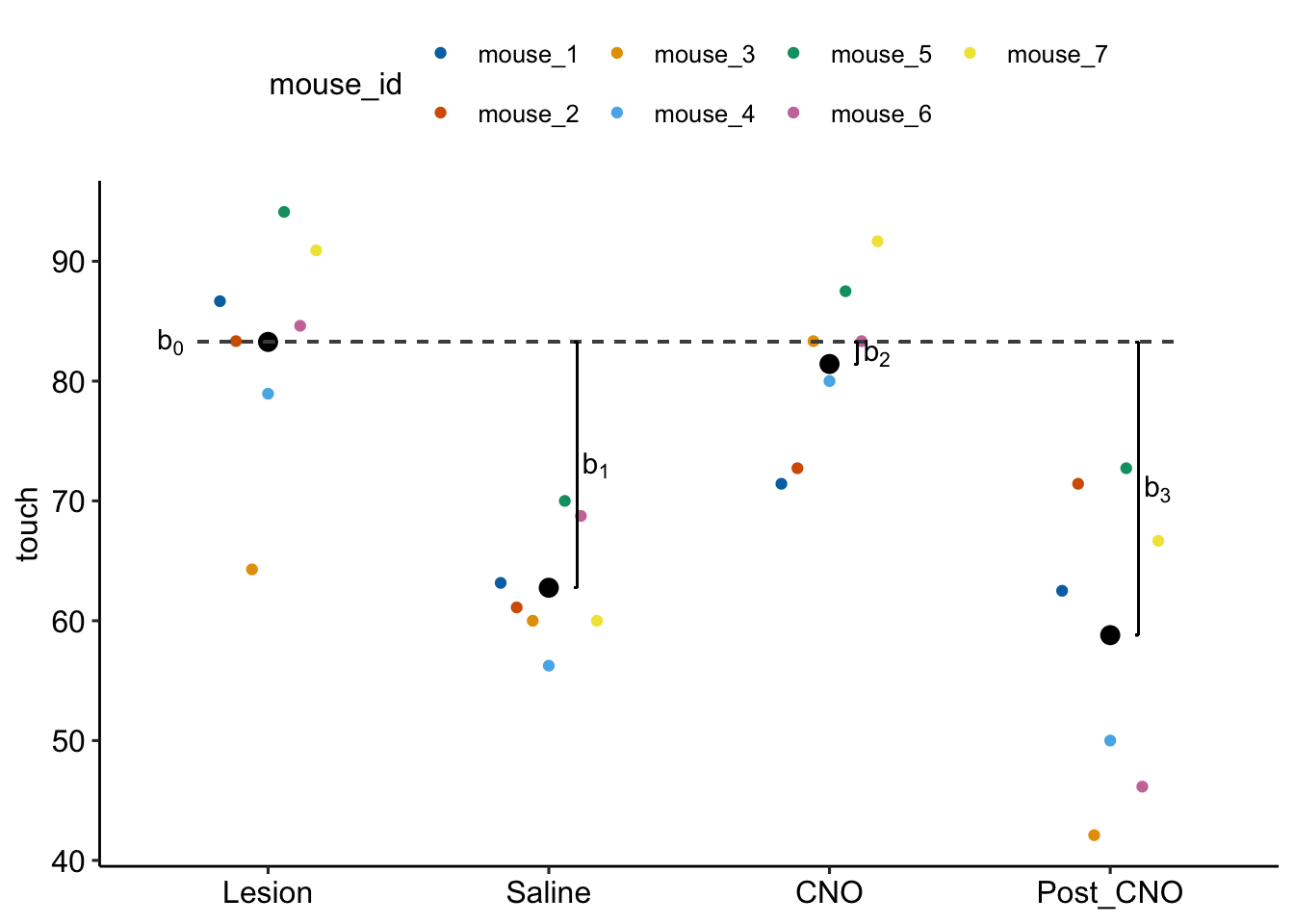
Fixed effects estimated by exp6g_m1. $b_0$ is the modeled mean of the Lesian treatment. $b_1$ is the difference (Saline - Lesian). $b_2$ is the difference (CNO - Lesian). $b_3$ is the difference (Post_CNO - Lesian).

Figure 16.9: Fixed effects estimated by exp6g_m1. $b_0$ is the modeled mean of the Lesian treatment. $b_1$ is the difference (Saline - Lesian). $b_2$ is the difference (CNO - Lesian). $b_3$ is the difference (Post_CNO - Lesian).

16.7.5 The random intercept coefficients of exp6g_m1

Table 16.6: Random intercept coefficients (g_0j) for exp6g_m1. For each mouse, the random intercept is the sum of the fixed intercept ($b_0$) and the random intercept effect $g_{0j}$.
mouse_id	random intercept	b_0	g_0j
mouse_1	82.874	83.268	-0.393
mouse_2	83.640	83.268	0.372
mouse_3	77.499	83.268	-5.769
mouse_4	79.943	83.268	-3.325
mouse_5	89.286	83.268	6.018
mouse_6	82.732	83.268	-0.536
mouse_7	86.901	83.268	3.633

Notes

The random intercept effect $g_{0j}$ is the difference between the modeled mean for mouse j and the mean of the reference treatment. Unlike the fixed intercept ($b_0$), $g_{0j}$ is an effect.
Figure ?? illustrates the random intercept coefficients $g_{0j}$ for model exp6g_m1.
The random intercept coefficients are often (but not always) treated as a source of nuisance variation – that is, the coefficients are not generally of interest and the values are not typically reported.

$Random intercept effects for model exp6g_m1. The pale, colored dots are the measured percent ipsilateral touch values for each mouse for each treatment. The dashed, gray lines are the modeled means for each treatment. The dashed grey line for the reference level ("Lesion") is the fixed intercept. The dark, colored dots at the reference level are the random intercepts. The value of each random intercept is the sum of the fixed intercept and the random intercept effect for that mouse. The vertical, colored line segments at the reference level are the random intercept effects $g_{0j}$. The length of the segment is the residual from the dashed, gray line to the pale dot. The random intercept effects for mice 1 and 2 are too short to see.$

Figure 16.10: Random intercept effects for model exp6g_m1. The pale, colored dots are the measured percent ipsilateral touch values for each mouse for each treatment. The dashed, gray lines are the modeled means for each treatment. The dashed grey line for the reference level (“Lesion”) is the fixed intercept. The dark, colored dots at the reference level are the random intercepts. The value of each random intercept is the sum of the fixed intercept and the random intercept effect for that mouse. The vertical, colored line segments at the reference level are the random intercept effects $g_{0j}$. The length of the segment is the residual from the dashed, gray line to the pale dot. The random intercept effects for mice 1 and 2 are too short to see.

16.7.6 The random and residual variance and the intraclass correlation of model exp6g_m1

##  Groups   Name        Std.Dev.
##  mouse_id (Intercept) 4.9882  
##  Residual             7.6155

Notes

The first element in “Std.Dev.” is the estimate of $\sqrt{\sigma^2_{0j}}$, the standard deviation among the donors due to the random effect of $\texttt{mouse_id}$.
The second element in “Std.Dev.” is $\sqrt{\sigma^2_{0}}$, the estimate of the standard deviation of the error variance ($\varepsilon^2$). Remember that the residuals of the model are the estimates of $\varepsilon$.
The ratio $\frac{\sigma^2_{0j}}{\sigma^2_{0j} + \sigma^2_{0}}$ (the ratio of the among-block variance to total random variance) is known as the intraclass correlation. This correlation is an estimate of the correlated error due to the by-mouse clustering if the model were fit without the added random intercept. For exp6g_m1, this correlation is 0.3.
The intraclass correlation ranges between 0 and 1 and makes a pretty good qualitative indicator of repeatability.

16.7.7 The linear mixed model exp6g_m1 increases precision of treatment effects, relative to a fixed effects model

Let’s compare the effects estimated by the linear mixed model exp6g_m1 with a linear model that ignores donor (a fixed effects model).

exp6g_m2 <- lm(touch ~ treatment, data = exp6g)

A. Inference from a linear mixed model with blocking factor (mouse_id) added as a random intercept. B. Inference from a fixed effects model.

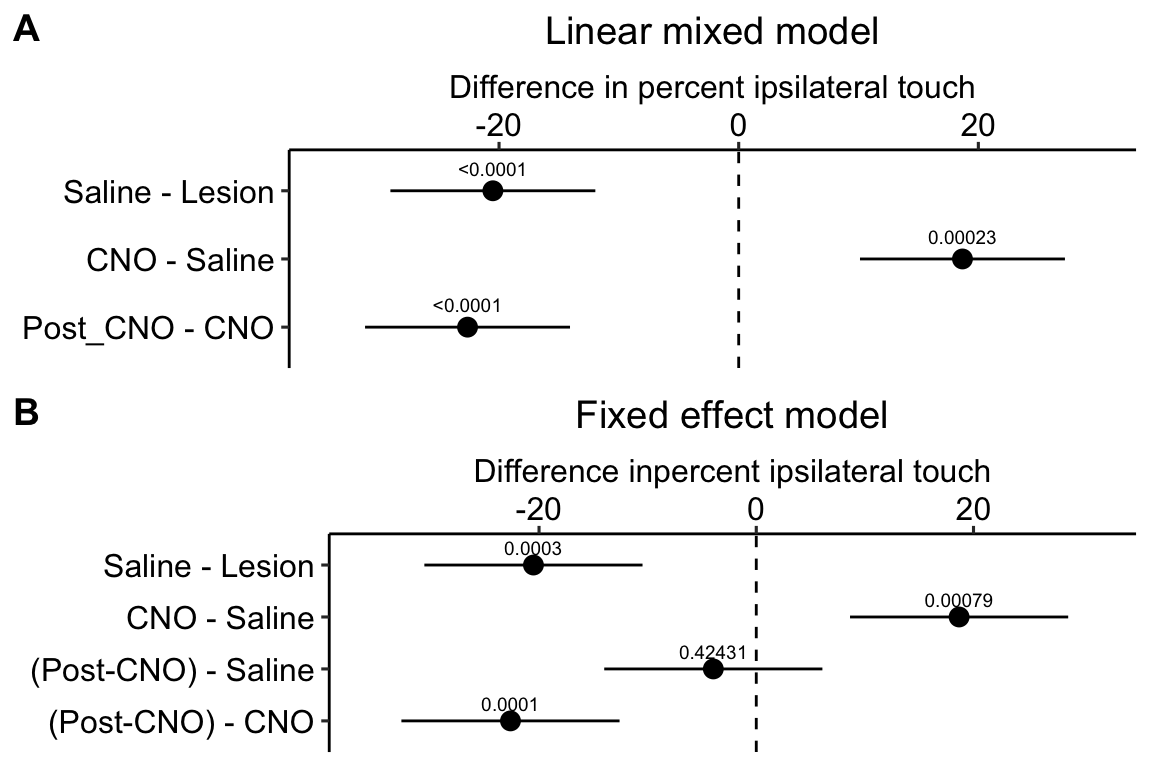
Figure 16.11: A. Inference from a linear mixed model with blocking factor (mouse_id) added as a random intercept. B. Inference from a fixed effects model.

Figure 16.11A is a plot of the effects from the linear mixed model exp6g_m1 that models the added variance due to mouse. Figure 16.11B is a plot of the effects from the fixed effect model exp6g_m2 that ignores the added variance due to mouse. The 95% confidence intervals of the treatment effects in model exp6g_m1 are slightly smaller than those in model exp6g_m2. Adding $\texttt{mouse_id}$ as a random factor to the linear model increases the precision of the estimate of the treatment effects by eliminating the among-mouse component of variance from the error variance.

The error variance (the estimate of $^2) in the linear mixed model and the fixed effects model is

summary(exp6g_m1)$sigma^2

## [1] 57.99549

summary(exp6g_m2)$sigma^2

## [1] 82.8777

The error variance is 43% higher in the fixed effects model. In the linear mixed model, the variance lost from the error was shifted to the random intercept. We can track this shift with the table of the two variance components of the linear mixed model, shown above, and here again (the values are the square roots of the variances).

VarCorr(exp6g_m1)

##  Groups   Name        Std.Dev.
##  mouse_id (Intercept) 4.9882  
##  Residual             7.6155

The sum of the two variance components of the linear mixed model is equal to the error variance of the fixed effects model:

sum(as.data.frame(VarCorr(exp6g_m1))$vcov)

## [1] 82.8777

16.7.8 Alternative models for exp6g

Linear mixed models are very flexible, a topic which is too advanced for this text. Here I want to focus on an alternative model because of its relevance to repeated measures ANOVA.

exp6g_m1a <- lmer(touch ~ treatment + (1 | mouse_id),
                 data = exp6g)
exp6g_m1b <- lme(touch ~ treatment,
                random = ~1|mouse_id,
                correlation = corSymm(form = ~ 1 | mouse_id),
                weights = varIdent(form = ~ 1 | treatment),
                data = exp6g)

Notes

Two models are fit. The two models have the same fixed effect but differ in how they model the random effect and the pattern of correlations in the residuals. The difference in specification determines the error variance and degrees of freedom for computing uncertainty. I’ll return to inference and the problem of “which model to choose” in a moment. First, how do these models differ?
Model exp6g_m1a is the same model analyzed and explained above. This model specifies a random intercept for each level of $\texttt{mouse_id}$.
Model exp6g_m1b has the same random effects as exp6g_m1a but adds two additional arguments, a correlation argument that explicitly models correlated error in the residuals and a weights argument that models heterogeneity in the residuals.
Consider the error (the residuals) of the fixed effect model touch ~ treatment cast into a matrix with the residuals for each treatment in its own column. This matrix of residuals will be a $7 \times 4$ (7 mice, 4 treatments) matrix that looks like the table of residuals in Example 1 (Table 16.1).
Model exp6g_m1a implicitly models compound symmetric correlated error. This means

the correlation between every pair of columns of the residual matrix is the same.
the variances of each of the columns of the residual matrix is the same.
Model exp6g_m1a assumes zero correlation among the columns of a residual matrix from Model exp6g_m1a. This is because the source of the correlated residuals from the fixed model has been modeled by the random intercept.

Model exp6g_m1b does not assume compound symmetric correlated error.

the argument correlation = corSymm(form = ~ 1 | mouse_id) in model exp6g_m1b explicitly models different correlations for all pairs of treatment combinations – that is, unstructured correlated error.
the argument weights = varIdent(form = ~ 1 | treatment) in model exp6g_m1b explicitly models heterogeneity in the residuals among the levels of $.

Model exp6g_m1b makes fewer assumptions for inference. The trade-off is the estimation of more parameters and the potential of overfitting.
A univariate model of a repeated measures ANOVA fit to the exp6g data is equivalent to model exp6g_m1a. See section 16.7.10.
A multivariate model of a repeated measures ANOVA fit to the exp6g data is equivalent to model exp6g_m1b. See section 16.7.11.

Table 16.7: Planned contrasts from the two alternative models.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
exp6g_m1a
Saline - Lesion	-20.52	4.071	18	-29.07	-11.96	-5.04	0.000085
CNO - Saline	18.67	4.071	18	10.12	27.23	4.59	0.000228
Post_CNO - CNO	-22.63	4.071	18	-31.18	-14.08	-5.56	0.000028
exp6g_m1b
Saline - Lesion	-20.52	3.172	18	-27.18	-13.85	-6.47	0.000004
CNO - Saline	18.67	3.057	18	12.25	25.10	6.11	0.000009
Post_CNO - CNO	-22.63	5.610	18	-34.42	-10.84	-4.03	0.000779

Planned comparisons of the two models are given in the tables above. The effect estimates are the same but inference differs quantitatively among the models (but not qualitatively) because of how each model models the error. Which model do we report? One way to evaluate the models is a statistic known as the AIC.

Table 16.8: AIC of the two alternative models fit to exp6g data
Model	AIC
exp6g_m1a	191.3367
exp6g_m1b	198.3888

AIC (Akaike Information Criterion) is a relative measure of model quality. Compare this to $R^2$, which is an absolute measure of goodness of fit. The AIC formula has two parts, one is a kind of goodness of fit (like $R^2$) and the other is a penalty based on the number of parameters in the model. As the goodness of fit increases, the AIC goes down. As the number of parameters increases, the AIC goes up. The model with the lowest AIC is the highest quality model. The actual number, however does not have any absolute meaning; it is only meaningful relative to the AICs computed from fits to different models using the same data.
The AICs of models exp6g_m1a and models exp6g_m1b suggest that model exp6g_m1b is too complex given the data. This has relevance for the repeated measures ANOVA analysis in the next section.

16.7.9 Paired t-tests and repeated measures ANOVA are special cases of linear mixed models

A paired t-test is a special case of linear mixed model fit to data from a randomized complete block design with no subsampling and only two treatment levels (see Lack of independence in the Violations chapter). A repeated measures ANOVA is a special case of linear mixed model fit to data from a randomized complete block design with no subsampling and more than two treatment levels (see Lack of independence in the Violations chapter).

Experiment 6g is a randomized complete block design with no subsampling and four treatments. A “which test” key in a traditional, experimental statistics textbook would guide a researcher to analyze these data using repeated measures ANOVA. There are two methods of repeated measures anova, the univariate model and the multivariate model.

16.7.10 Classical (“univariate model”) repeated measures ANOVA of exp6g

exp6g_aov1 <- aov_4(touch ~ treatment +
                    (treatment | mouse_id),
                  data = exp6g)

Table 16.9: Planned contrasts for the linear mixed model exp6g_m1a and the univariate model of the repeated measures ANOVA.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
exp6g_m1a
Saline - Lesion	-20.52	4.071	18	-29.07	-11.96	-5.04	0.000085
CNO - Saline	18.67	4.071	18	10.12	27.23	4.59	0.000228
Post_CNO - CNO	-22.63	4.071	18	-31.18	-14.08	-5.56	0.000028
univariate RM-ANOVA
Saline - Lesion	-20.52	3.172	6	-28.28	-12.75	-6.47	0.000649
CNO - Saline	18.67	3.057	6	11.19	26.15	6.11	0.000877
Post_CNO - CNO	-22.63	5.610	6	-36.36	-8.90	-4.03	0.006853

Notes

In addition to the assumptions of the linear model outlined in the Violations chapter, the classical (“univariate model”) repeated measures ANOVA assumes sphericity, which is the equality of the variances of all pairwise differences among treatment combinations.
The univariate model of the classic RM ANOVA is equivalent to Model exp6g_m1a.

16.7.11 “Multivariate model” repeated measures ANOVA

Table 16.10: Planned contrasts for the linear mixed model exp6g_m1b and the multivariate model of the repeated measures ANOVA.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
exp6g_m1b
Saline - Lesion	-20.52	3.172	18	-27.18	-13.85	-6.47	0.000004
CNO - Saline	18.67	3.057	18	12.25	25.10	6.11	0.000009
Post_CNO - CNO	-22.63	5.610	18	-34.42	-10.84	-4.03	0.000779
multivariate RM-ANOVA
Saline - Lesion	-20.52	3.172	6	-28.28	-12.75	-6.47	0.000649
CNO - Saline	18.67	3.057	6	11.19	26.15	6.11	0.000877
Post_CNO - CNO	-22.63	5.610	6	-36.36	-8.90	-4.03	0.006853

Notes

The sphericity assumption of classical repeated measures ANOVA is relaxed if the model is fit using the “multivariate model”.
The multivariate model repeated measures ANOVA is a linear model with a multivariate response and not a linear mixed model. In the multivariate model, each treatment combination is a different response variable and there is a single row for each level of the random factor ($\texttt{mouse_id}$ in Experiment 6g). The multivariate model is a different way of handling the correlated error that occurs when conceiving of the design as univariate.
The multivariate repeated measures ANOVA is equivalent to the linear mixed model exp6g_m1b. The SEs of the contrasts are the same but the degrees of freedom differ. Because of the increased df of the linear mixed model, the CIs are narrower and the p-value is smaller – that is the linear mixed model is less conservative than the repeated measures ANOVA. There is no correct degrees of freedom for a linear mixed model like this and emmeans outputs one way to compute these (with options for others, none of which are equivalent to those from the multivariate model RM-ANOVA).

16.7.12 Linear mixed models vs repeated measures ANOVA

Many modern textbooks encourage researchers to use linear mixed models instead of repeated measures ANOVA for randomized complete block designs (with or without subsampling) because

linear mixed models do not exclude random units (subject/mouse/donor/cage) with missing measures of one of the treatment combinations. Example 2 (diHOME exp2a) – A repeated measures ANOVA is a special case of a linear mixed model is an example of this kind of missing data.
if there is subsampling, linear mixed models do not aggregate the random-unit data, that is, linear mixed models do not simply compute the means and ignore the variance of the sample within each random unit.
linear mixed models allow for modeling additional sources of correlated error, that is, an experiment may have two or more random factor variables (for example, donor and experiment).
linear mixed models allow a researcher to model different patterns of correlated error. This is especially important in longitudinal experiments.
linear mixed models can be generalized to model sampling from non-normal distributions – these are generalized linear mixed models.

16.7.13 Modeling $\texttt{mouse_id}$ as a fixed effect

\[ \begin{equation} \texttt{touch} \sim \texttt{treatment + mouse_id} \end{equation} \tag{16.3} \]

Model (16.3) (using R formula syntax) is a linear model with the block $\texttt{mouse_id}$ added as a fixed covariate instead of a random intercept. The coefficients of the fit model are

exp6g_m3 <- lm(touch ~ treatment + mouse_id,
               data = exp6g)

exp6g_m3_coef <- cbind(coef(summary(exp6g_m3)),
                       confint(exp6g_m3))

	Estimate	Std. Error	t value	Pr(>\|t\|)	2.5 %	97.5 %
(Intercept)	82.65	4.551	18.2	0.0000	73.08	92.21
treatmentSaline	-20.52	4.071	-5.0	0.0001	-29.07	-11.96
treatmentCNO	-1.84	4.071	-0.5	0.6565	-10.39	6.71
treatmentPost_CNO	-24.47	4.071	-6.0	0.0000	-33.02	-15.92
mouse_idmouse_2	1.21	5.385	0.2	0.8245	-10.10	12.52
mouse_idmouse_3	-8.51	5.385	-1.6	0.1315	-19.82	2.81
mouse_idmouse_4	-4.64	5.385	-0.9	0.4003	-15.95	6.67
mouse_idmouse_5	10.15	5.385	1.9	0.0758	-1.17	21.46
mouse_idmouse_6	-0.23	5.385	0.0	0.9671	-11.54	11.09
mouse_idmouse_7	6.37	5.385	1.2	0.2521	-4.94	17.69

Notes

The coefficients include a slope for the seven non-reference levels of mouse_id We typically don’t care about these.
In a randomized complete block design with only 1 replicate of each treatment combination per block, like that in Experiment 6g, inference about treatment effects is exactly that same between this model and the random intercept model exp6g_m1. Compare the SE, CI and p-value for the coefficients of the treatment effects to those from the linear mixed model exp6g_m1.

	Estimate	Std. Error	df	t value	Pr(>\|t\|)	2.5 %	97.5 %
(Intercept)	83.27	3.441	18.9	24.20	0.0000	76.72	89.81
treatmentSaline	-20.52	4.071	18.0	-5.04	0.0001	-28.25	-12.78
treatmentCNO	-1.84	4.071	18.0	-0.45	0.6565	-9.58	5.90
treatmentPost_CNO	-24.47	4.071	18.0	-6.01	0.0000	-32.21	-16.73

In a randomized complete block design with only 1 replicate of each treatment combination per block, like that in Experiment 6g, inference about treatment means differs between this model and the random intercept model – the SE of the means of the fixed effect model are smaller than the SE of the means of the linear mixed model. Compare the SE and CI of the (Intercept) (the mean of the reference treatment combination) between the fixed effect and linear mixed model.
The equivalence of inference in the treatment effect between the fixed effect and linear mixed model holds only for balanced randomized complete block designs – where all blocks contain all treatment combinations and the subsampling replicate size is the same for all treatment combinations for all blocks. This means, outside of special cases like Experiment 6g, the choice between adding a blocking variable as a random or fixed factor depends on assumptions about the model.

16.8 Example 3 – Factorial experiments and no subsampling replicates (exp5c)

Example 3 is similar to example 2 in that there is no subsampling replication and we cannot add random slopes to the linear mixed model. Example 3 differs in that the design is factorial – there are two, crossed fixed factors. Consequently, there are several alternative models with different sets of random intercepts. The reported model includes two random intercepts, one of which models differences in batch effects among treatment levels (treatment by batch interactions). This interaction intercept is an alternative to random slope for modeling treatment by batch interactions.

Transcriptomic profiling of skeletal muscle adaptations to exercise and inactivity

Source figure: Fig. 5c

Source data: Source Data Fig. 5

16.8.1 Understand the data

The data for Example 1 are from Figure 5c. Six muscle source cells were used to start six independent cultures. Cells from each culture were treated with either a negative control (“Scr”) or a siRNA (“siNR4A3”) that “silences” expression of the NR4A3 gene product by cleaving the mRNA. Glucose uptake in the two cell types was measured at rest (“Basal”) and during electrical pulse stimulation (“EPS”).

The design is a $2 \times 2$ Randomized complete block with no subsampling. There are two factors each with two levels: $\texttt{treatment}$ (“Scr”, “siNR4A3”) and $\texttt{activity}$ (“Basal”, “EPS”). Each source cell is a block. All four treatment combinations were measured once per block.

16.8.2 Examine the data

The plot shows a strong donor effect.

16.8.3 Model fit and inference

exp5c_m1a <- lmer(glucose_uptake ~ treatment * activity +
                   (1 | donor),
                 data = exp5c)

exp5c_m1b <- lmer(glucose_uptake ~ treatment * activity +
                   (1 | donor) +
                   (1 | donor:treatment) +
                   (1 | donor:activity),
                 data = exp5c)

exp5c_m1c <- lmer(glucose_uptake ~ treatment * activity +
                   (1 | donor) +
                   (1 | donor:treatment),
                 data = exp5c)

exp5c_m1d <- lme(glucose_uptake ~ treatment * activity,
                 random =  ~ 1 | donor,
                 correlation = corSymm(form = ~ 1 | donor),
                 weights = varIdent(form = ~ 1|t.by.a),
                 data = exp5c)

# check AIC
AIC(exp5c_m1a, exp5c_m1b, exp5c_m1c, exp5c_m1d)

##           df       AIC
## exp5c_m1a  6  8.153813
## exp5c_m1b  8 10.052676
## exp5c_m1c  7  8.052676
## exp5c_m1d 15 14.763024

# check VarCorr model c
VarCorr(exp5c_m1c) # fine

##  Groups          Name        Std.Dev.
##  donor:treatment (Intercept) 0.089519
##  donor           (Intercept) 0.352097
##  Residual                    0.090685

# report 1c (based on AIC and VarCorr check)
exp5c_m1 <- exp5c_m1c

exp5c_m1b (equivalent to univariate repeated measures ANOVA) is singular fit. don’t use. Trivial difference in AIC between exp5c_m1a and exp5c_m1c. Nothing in VarCorr with exp5c_m1c raises red flags. Report exp5c_m1c.

16.8.3.1 Check the model

ggcheck_the_model(exp5c_m1)

fine.

16.8.3.2 Inference from the model

exp5c_m1_coef <- cbind(coef(summary(exp5c_m1)),
                       confint(exp5c_m1)[-c(1:3),])

exp5c_m1_coef %>%
  kable(digits = c(2,3,1,1,4,2,2)) %>%
  kable_styling()

	Estimate	Std. Error	df	t value	Pr(>\|t\|)	2.5 %	97.5 %
(Intercept)	1.34	0.153	5.8	8.8	0.0001	1.02	1.66
treatmentsiNR4A3	0.08	0.074	8.5	1.1	0.2994	-0.07	0.23
activityEPS	0.15	0.052	10.0	2.9	0.0163	0.05	0.25
treatmentsiNR4A3:activityEPS	-0.27	0.074	10.0	-3.6	0.0048	-0.41	-0.12

exp5c_m1_emm <- emmeans(exp5c_m1, specs = c("treatment", "activity"))

treatment	activity	emmean	SE	df	lower.CL	upper.CL
Scr	Basal	1.34	0.153	5.8	0.96	1.72
siNR4A3	Basal	1.42	0.153	5.8	1.04	1.80
Scr	EPS	1.49	0.153	5.8	1.11	1.87
siNR4A3	EPS	1.31	0.153	5.8	0.93	1.68

# exp5c_emm # print in console to get row numbers
# set the mean as the row number from the emmeans table
scr_basal <- c(1,0,0,0)
siNR4A3_basal <- c(0,1,0,0)
scr_eps <- c(0,0,1,0)
siNR4A3_eps <- c(0,0,0,1)

exp5c_m1_planned <- contrast(exp5c_m1_emm,
                       method = list(
                         "(Scr EPS) - (Scr Basal)" = c(scr_eps - scr_basal),
                         "(siNR4A3 EPS) - (siNR4A3 Basal)" = c(siNR4A3_eps - siNR4A3_basal),
                         "Interaction" = c(siNR4A3_eps - siNR4A3_basal) -
                           c(scr_eps - scr_basal)
                           
                       ),
                       adjust = "none"
) %>%
  summary(infer = TRUE)

contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
(Scr EPS) - (Scr Basal)	0.15	0.052	10	0.03	0.27	2.88	0.016
(siNR4A3 EPS) - (siNR4A3 Basal)	-0.12	0.052	10	-0.23	0.00	-2.22	0.051
Interaction	-0.27	0.074	10	-0.43	-0.10	-3.61	0.005

16.8.3.3 Plot the model

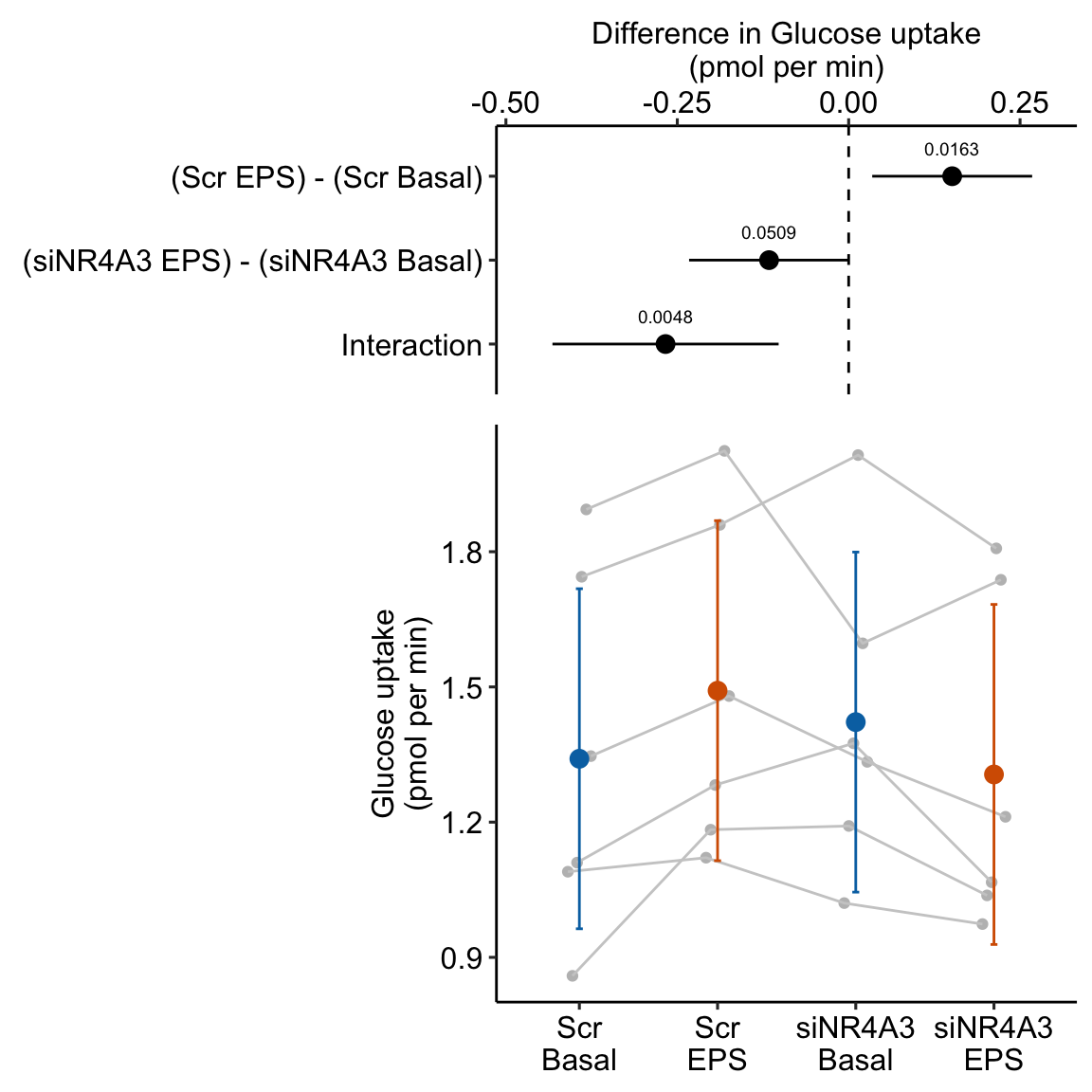
Figure 16.12: Treatment effect on glucose uptake. Gray dots connected by lines are individual donors.

16.8.3.4 Alternaplot the model

Glucose response to different treatments. Gray dots connected by lines are individual donors. Dashed gray line is expected additive mean of "siNR4A3 EPS".

Figure 16.13: Glucose response to different treatments. Gray dots connected by lines are individual donors. Dashed gray line is expected additive mean of “siNR4A3 EPS”.

Notes

Many researchers might look at the wide confidence intervals relative to the short distance between the means and think “no effect”. The confidence intervals are correct, they simply are not meant to be tools for inferring anything about differences in means. This is one of many reasons why plots of means and error bars can be misleading for inference, despite the ubiquity of their use for communicating results. And, its why I prefer the effects-and-response plots, which explicitly communicate correct inference about effects.

16.8.4 Why we care about modeling batch in exp5c

Figure 16.14 shows the modeled means of the four treatment combinations and the individual values colored by donor. It is pretty easy to see that the glucose uptake values for donors 4 and 5 are well above the mean for all four treatments. And, the values for donors 1, 2, and 3 are well below the mean for all four treatments. The values for donor 6 are near the mean for all four treatments.

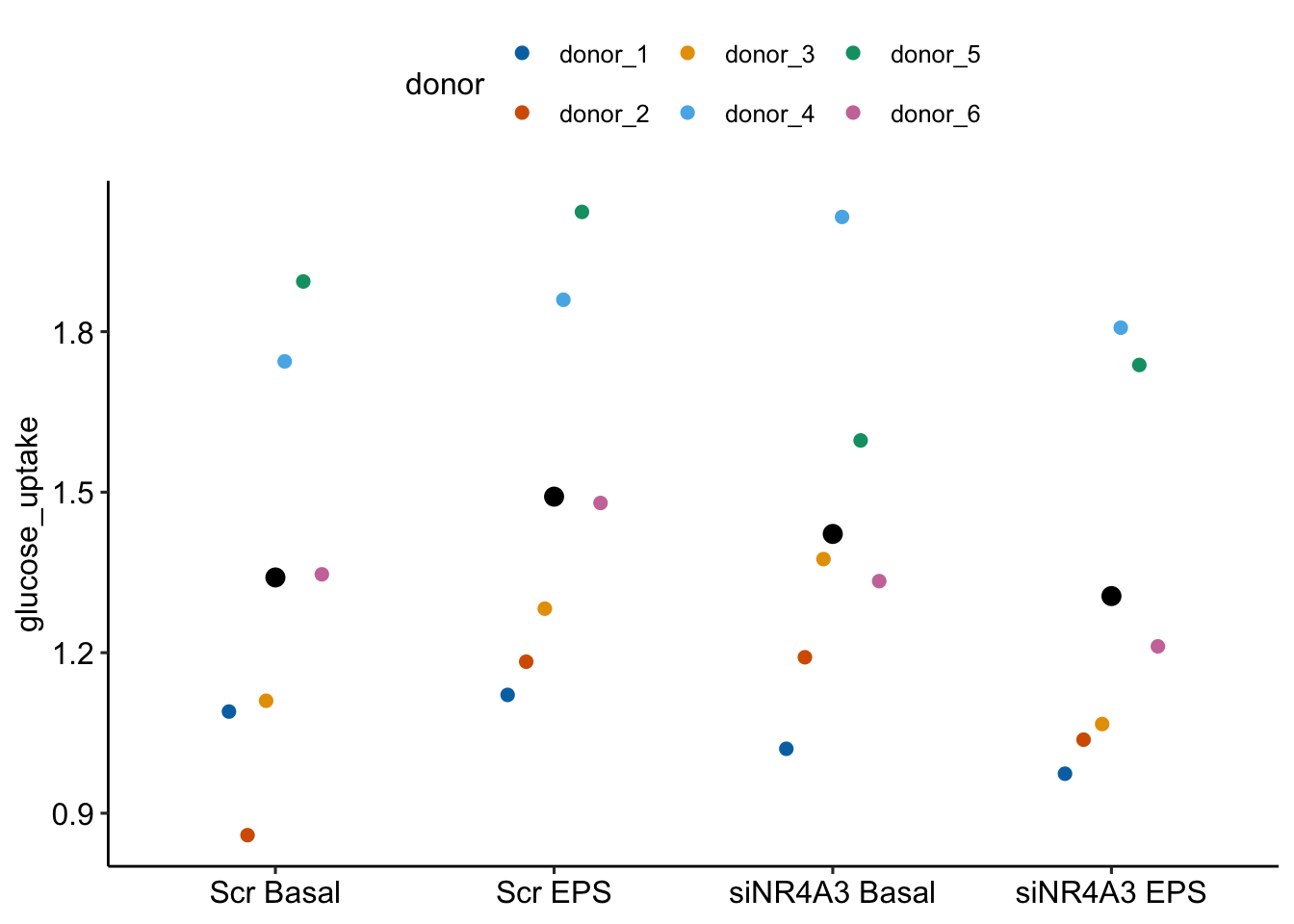
Why we care about blocking. The black dots are the modeled means of each treatment combination. The colored dots are the measured values of the response for each donor. The position of a donor relative to the mean is easy to see with these data.

Figure 16.14: Why we care about blocking. The black dots are the modeled means of each treatment combination. The colored dots are the measured values of the response for each donor. The position of a donor relative to the mean is easy to see with these data.

Let’s compare the effects estimated by the linear mixed model exp5c_m1 with a linear model that ignores donor.

exp5c_m2 <- lm(glucose_uptake ~ treatment * activity,
           data = exp5c)

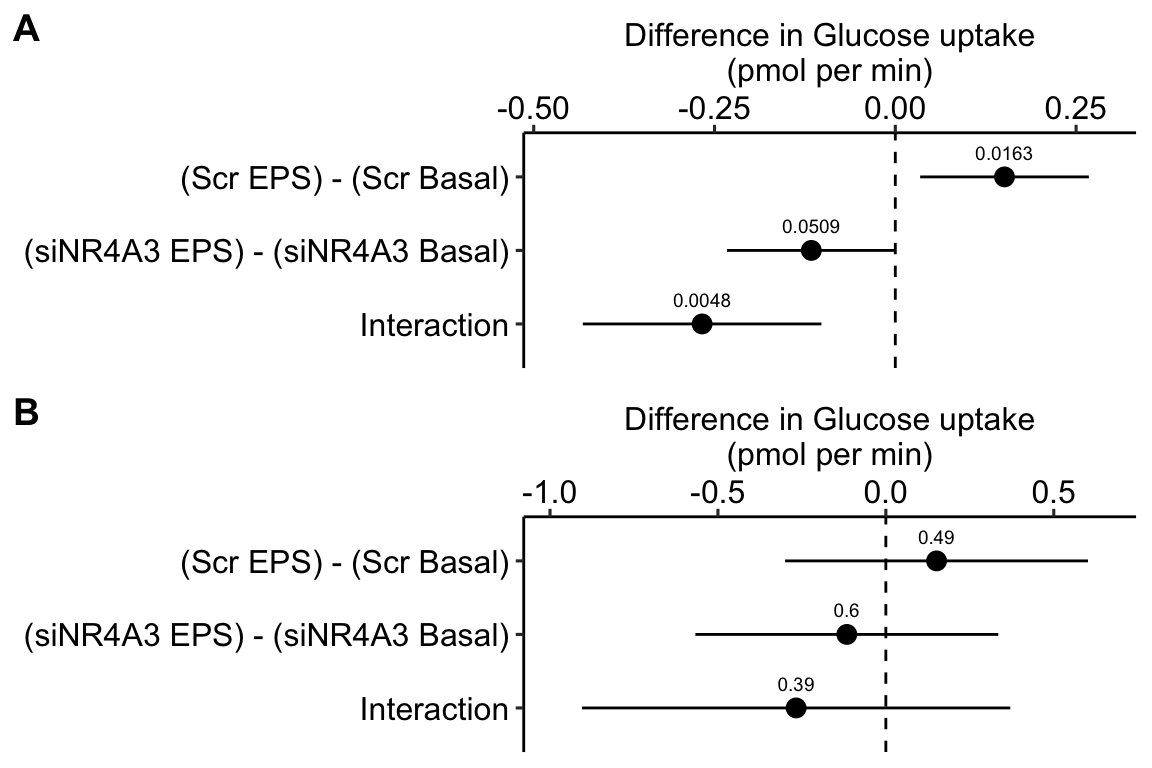
Figure 16.15: A. Inference from a linear mixed model with blocking factor (donor) added as a random intercept. B. Inference from a fixed effects model.

Figure 16.15A is a plot of the effects from the linear mixed model that models the correlated error due to donor. Figure 16.15B is a plot of the effects from the fixed effect model that ignores the correlated error due to donor. Adding $\texttt{donor}$ as a factor to the linear model increases the precision of the estimate of the treatment effects by eliminating the among-donor component of variance from the error variance.

16.8.5 The linear mixed model exp5c_m1 adds two random intercepts

There are two random intercepts in the linear mixed model exp5c_m1 fit to the exp5c data (exp5c_m1 is copied from exp5c_m1c in Model fit and inference).

\[ \begin{align} \texttt{glucose_uptake}_j = \ &(\beta_0 + \gamma_{0j} + \gamma_{0jk}) + \beta_1 (\texttt{treatment}_\texttt{siNR4A3}) + \beta_2 (\texttt{activity}_\texttt{EPS}) \ + \\ &\beta_3 (\texttt{treatment}_\texttt{siNR4A3}:\texttt{activity}_\texttt{EPS}) + \varepsilon \end{align} \tag{16.4} \]

The random intercept effect $\gamma_{0j}$ models donor variation in the reference level. j indexes donor j. A coefficient is estimated for each donor.
The random intercept effect $\gamma_{0jk}$ models the variation due to the $\texttt{donor}$ by $\texttt{treatment}$ combinations. A coefficient is estimated for each of the 6 (donors) $\times$ 2 (levels of $\texttt{treatment}$). k indexes treatment level k. This interaction intercept is an alternative to random slope for modeling treatment by batch interactions. Unlike a random slope, there is a $\gamma_{0jk}$ coefficient for each donor in the reference level.

16.8.6 The fixed effect coefficients of model exp5c_m1

The fixed effect coefficients of model exp5c_m1 are

	Estimate	Std. Error	df	t value	Pr(>\|t\|)	2.5 %	97.5 %
(Intercept)	1.34	0.153	5.8	8.77	0.0001	1.02	1.66
treatmentsiNR4A3	0.08	0.074	8.5	1.11	0.2994	-0.07	0.23
activityEPS	0.15	0.052	10.0	2.88	0.0163	0.05	0.25
treatmentsiNR4A3:activityEPS	-0.27	0.074	10.0	-3.61	0.0048	-0.41	-0.12

Notes

The interpretation of the fixed effectcs coefficients have the usual interpretation for a factorial linear model. Figure 16.16 is a reminder.

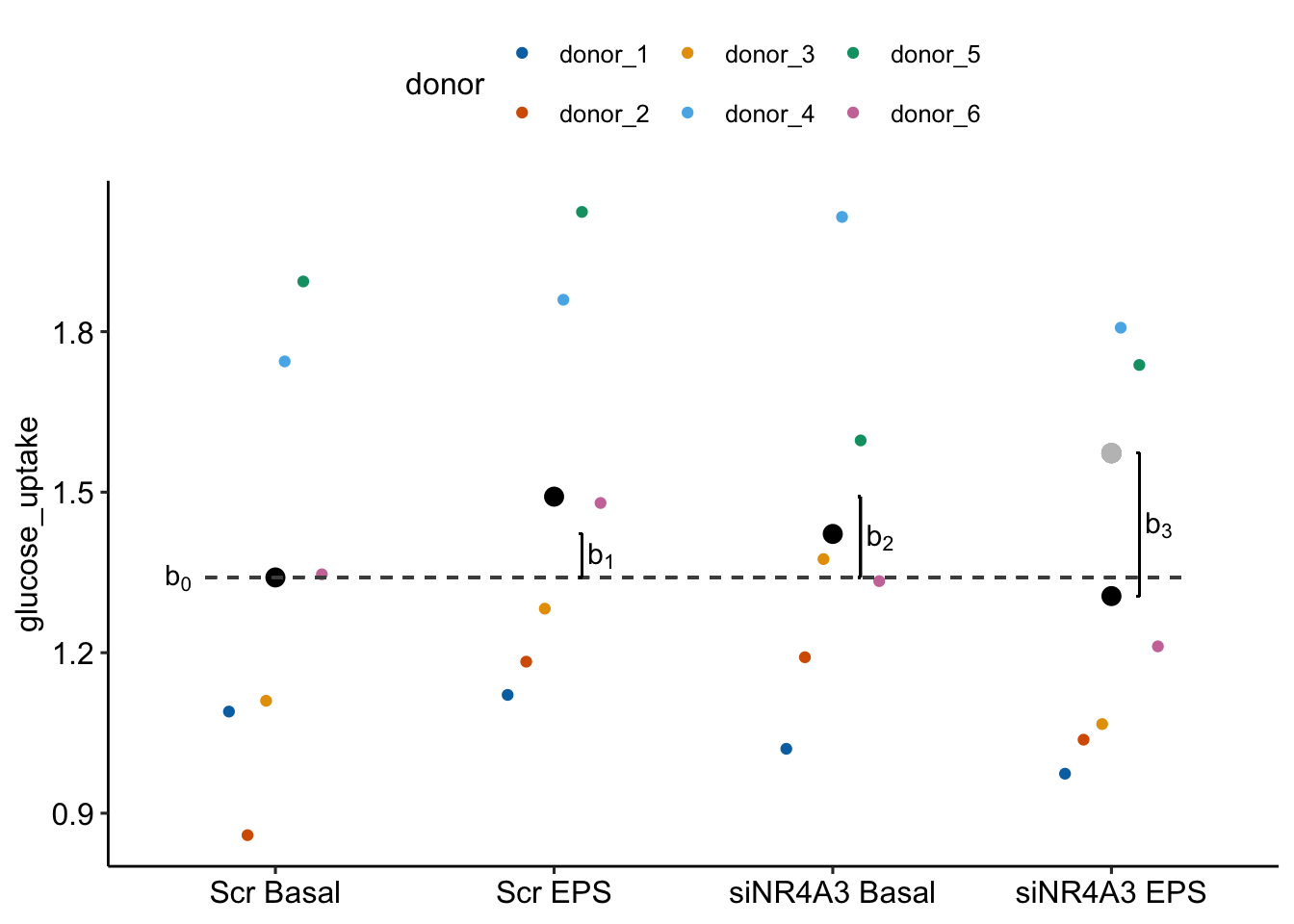
Fixed effects estimated by exp5c_m1. The light gray point is the expected value of the GPR174- F treatment if genotype and sex were additive.

Figure 16.16: Fixed effects estimated by exp5c_m1. The light gray point is the expected value of the GPR174- F treatment if genotype and sex were additive.

16.8.7 The random effect coefficients of model exp5c_m1

Table 16.11: Random intercept effects for each donor (g_0j) and for each donor:treatment combination (g_0jk) for exp5c_m1. There are two random intercepts. random_intercept_j is the sum of the fixed intercept (b_0) and g_0j. random_intercept_jk is the sum of the fixed intercept (b_0) and g_0jk.
donor:treatment	random_intercept_j	random_intercept_jk	b_0	g_0j	g_0jk
donor_1:Scr	1.018	1.349	1.341	-0.323	0.008
donor_1:siNR4A3	1.018	1.312	1.341	-0.323	-0.029
donor_2:Scr	1.033	1.283	1.341	-0.307	-0.058
donor_2:siNR4A3	1.033	1.379	1.341	-0.307	0.038
donor_3:Scr	1.168	1.310	1.341	-0.173	-0.031
donor_3:siNR4A3	1.168	1.360	1.341	-0.173	0.020
donor_4:Scr	1.785	1.302	1.341	0.445	-0.039
donor_4:siNR4A3	1.785	1.408	1.341	0.445	0.068
donor_5:Scr	1.744	1.433	1.341	0.403	0.092
donor_5:siNR4A3	1.744	1.275	1.341	0.403	-0.066
donor_6:Scr	1.296	1.368	1.341	-0.045	0.028
donor_6:siNR4A3	1.296	1.310	1.341	-0.045	-0.031

Notes

The random intercept “random_intercept_j” is the sum of the fixed intercept $b_0$ and the random intercept effect $g_{0j}$ for donor j. The $g_{0j}$ estimate the $\gamma_{0j}$ in Model (16.4). Note that $g_{0j}$ is the same for both treatment levels within a donor. The illustration of these random effects is similar to that for Example 2 exp6g_m1 (Figure 16.10.
The random intercept “random_intercept_jk” is the sum of the fixed intercept $b_0$ and the random intercept effect $g_{0jk}$ for donor j in treatment level k (with the reference level equal to 1). The $g_{0jk}$ estimate the $\gamma_{0jk}$ in Model (16.4). The $g_{0jk}$ differ for each combination of $\texttt{donor}$ and $\texttt{treatment}$.
The donor:treatment random intercepts (“random_intercept_jk”) are shown with the dark, colored dots in Figure 16.17A. The distance from the dark colored dot to the dashed, gray line (the modeled mean for the treatment:activity combination) is the random intercept effect estimate of $\gamma_{0jk}$.
The set of random intercept effects for the donor:treatment combinations ($g_{0jk}$) are the same between the two activity levels. This is seen in Figure 16.17A - compare the pattern of dark, colored dots in the two EPS treatments to the two Basal treatments.
The combined random intercept effects ($g_{0j} + g_{0jk}$) are shown in Figure 16.17B as the distance between the dark, colored dots and the dashed, gray lines.
There is some communication decision-making in Figure 16.17. The actual y-values of the dark, colored dots are the random intercept effect plus the treatment-combination modeled mean. Thus, in A, the dark colored dots are equal to “random_intercept_jk” only at the reference level (since the reference model mean is the fixed intercept).

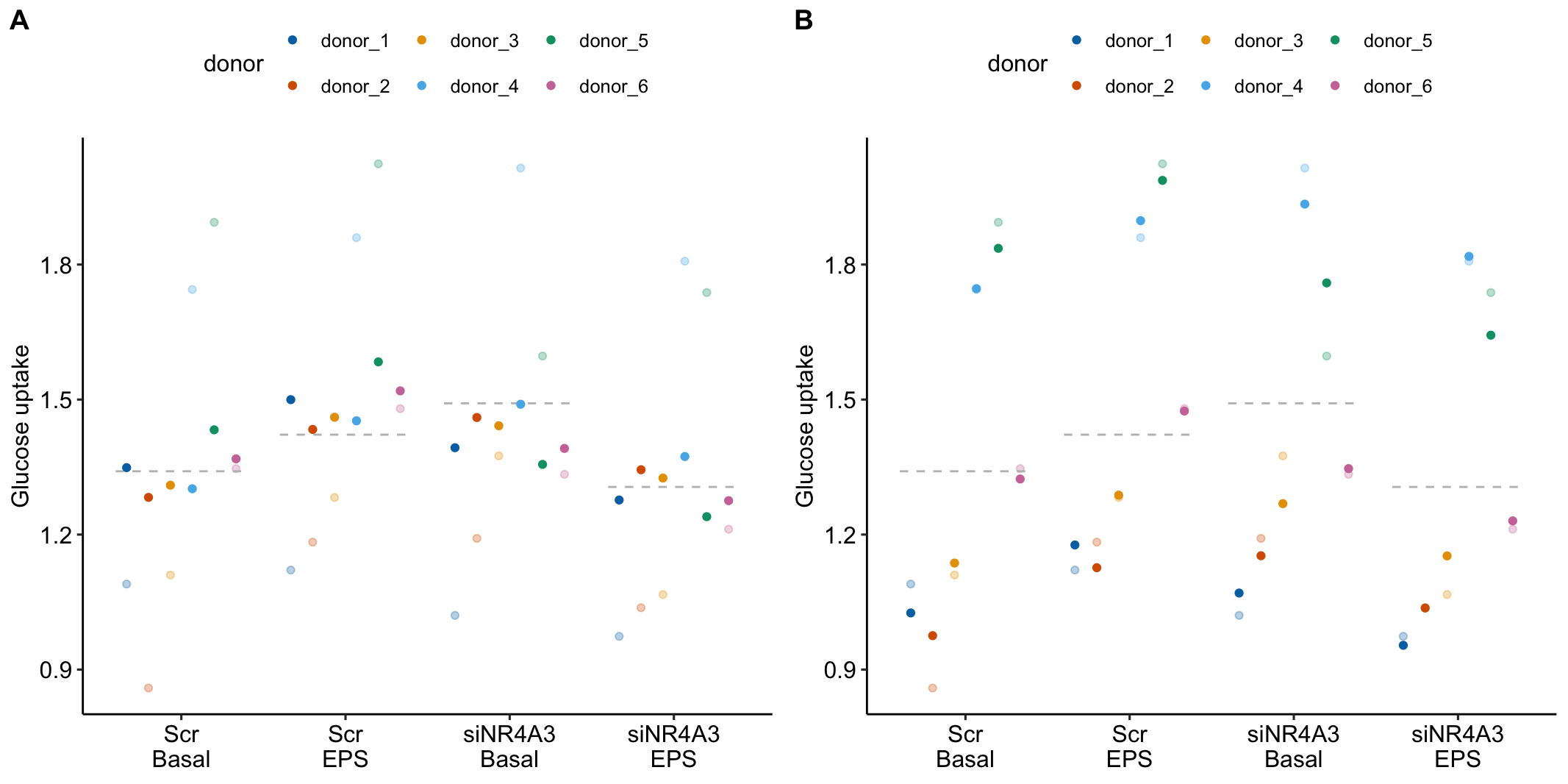
$Random intercepts for model exp5c_m1. The pale, colored dots are the measured glucose uptake values for each donor at each treatment combination. The dashed, gray lines are the modeled means for each treatment combination. (A) The distance from a dark colored dot to the dashed, gray line is the random intercept effect $g_{0jk}$. (B) The distance from a dark colored dot to the dashed, gray line is the combined random intercept effect $g_{0j} + g_{0jk}$.$

Figure 16.17: Random intercepts for model exp5c_m1. The pale, colored dots are the measured glucose uptake values for each donor at each treatment combination. The dashed, gray lines are the modeled means for each treatment combination. (A) The distance from a dark colored dot to the dashed, gray line is the random intercept effect $g_{0jk}$. (B) The distance from a dark colored dot to the dashed, gray line is the combined random intercept effect $g_{0j} + g_{0jk}$.

16.8.8 Alternative models for exp5c

exp5c_m1a <- lmer(glucose_uptake ~ treatment * activity +
                   (1 | donor),
                 data = exp5c)

exp5c_m1b <- lmer(glucose_uptake ~ treatment * activity +
                   (1 | donor) +
                   (1 | donor:treatment) +
                   (1 | donor:activity),
                 data = exp5c)

## boundary (singular) fit: see help('isSingular')

exp5c_m1c <- lmer(glucose_uptake ~ treatment * activity +
                   (1 | donor) +
                   (1 | donor:treatment),
                 data = exp5c)

exp5c_m1d <- lme(glucose_uptake ~ treatment * activity,
                 random =  ~ 1 | donor,
                 correlation = corSymm(form = ~ 1 | donor),
                 weights = varIdent(form = ~ 1|t.by.a),
                 data = exp5c)

Notes

Four models are fit. The models specify the same fixed effects but different random effects or patterns of correlated error. Again, we care about the fixed effects – this is the point of the experiment – but the specification of the random effects determines the error variance and degrees of freedom for computing uncertainty.
Model exp5c_m1a specifies a random intercept for each level of $\texttt{donor}$.
Model exp5c_m1b adds two additional random intercepts to Model exp5c_m1a. The code (1 | donor:treatment) adds an intercept for each combination of $\texttt{donor}$ and $\texttt{treatment}$. The code (1 | donor:activity) adds an intercept for each combination of $\texttt{donor}$ and $\texttt{activity}$. This model is the equivalent of the univariate model of a repeated measures ANOVA of these data (see Classical (“univariate model”) repeated measures ANOVA below).
Model exp5c_m1c adds only one additional random intercept ((1 | donor:treatment)). It is a simplification of Model exp5c_m1c. This is the model reported and explained above.
Model exp5c_m1d has the same random effects as exp5c_m1a but models unstructured correlated error and heterogeneity of the error, as described for Example 2: Alternative models for exp6g. This model is equivalent to the multivariate model of a repeated measures ANOVA of these data (see “Multivariate model” repeated measures ANOVA below).
lmer returns a message “boundary (singular) fit: see ?isSingular” for exp5c_m1b. The model was fit but the message means that we should be cautious about (or simply avoid) interpreting any inferential statistics (SEs, CIs, p-values). Looking at the estimates of the estimated parameters of the random effects in the table below (the variances of the effects and the covariances among the effects), Model exp5c_m1b estimates zero variance for the $\texttt{donor:activity}$ random intercept. This suggests that we could simplify exp5c_m1b by removing (1 | donor:activity) from the model – this is exp5c_m1c. Think about this warning. If we fit using repeated measures ANOVA (next section), we won’t get a warning message but we still may be overfitting.

VarCorr(exp5c_m1b)

##  Groups          Name        Std.Dev.
##  donor:activity  (Intercept) 0.000000
##  donor:treatment (Intercept) 0.089519
##  donor           (Intercept) 0.352092
##  Residual                    0.090686

Planned comparisons of the four alternative models are given in Table 16.12. The effect estimates are the same but inference differs slightly among the models because of how each model partitions error variance to either random effects or the residuals.

Table 16.12: Planned contrasts from the four alternative models.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
exp5c_m1a
(Scr EPS) - (Scr Basal)	0.15	0.067	15	0.01	0.29	2.25	0.040
(siNR4A3 EPS) - (siNR4A3 Basal)	-0.12	0.067	15	-0.26	0.03	-1.73	0.105
Interaction	-0.27	0.095	15	-0.47	-0.06	-2.81	0.013
exp5c_m1b
(Scr EPS) - (Scr Basal)	0.15	0.052	10	0.03	0.27	2.88	0.016
(siNR4A3 EPS) - (siNR4A3 Basal)	-0.12	0.052	10	-0.23	0.00	-2.22	0.051
Interaction	-0.27	0.074	5	-0.46	-0.08	-3.61	0.015
exp5c_m1c
(Scr EPS) - (Scr Basal)	0.15	0.052	10	0.03	0.27	2.88	0.016
(siNR4A3 EPS) - (siNR4A3 Basal)	-0.12	0.052	10	-0.23	0.00	-2.22	0.051
Interaction	-0.27	0.074	10	-0.43	-0.10	-3.61	0.005
exp5c_m1d
(Scr EPS) - (Scr Basal)	0.15	0.040	15	0.07	0.24	3.82	0.002
(siNR4A3 EPS) - (siNR4A3 Basal)	-0.12	0.063	15	-0.25	0.02	-1.85	0.083
Interaction	-0.27	0.083	15	-0.44	-0.09	-3.22	0.006

Table 16.13: AIC of the four alternative models firt to exp5c data
Model	AIC
exp5c_m1a	8.153813
exp5c_m1b	10.052675
exp5c_m1c	8.052675
exp5c_m1d	14.763024

The use of AIC for selecting among models with different random effects was described above. The AICs of the models suggest that models exp5c_m1b and exp5c_m1d are too complex given the data. The AICs of models exp5c_m1a and exp5c_m1c are effectively the same. I reported exp5c_m1c simply to allow me to explain the donor:treatment random effect.

16.8.9 Classical (“univariate model”) repeated measures ANOVA

exp5c_aov1 <- aov_4(glucose_uptake ~ treatment * activity +
                    (treatment * activity | donor),
                  data = exp5c)

Table 16.14: Planned contrasts for the linear mixed model exp5c_m1c and the univariate model of the repeated measures ANOVA.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
exp5c_m1c
(Scr EPS) - (Scr Basal)	0.15	0.052	10	0.03	0.27	2.88	0.016
(siNR4A3 EPS) - (siNR4A3 Basal)	-0.12	0.052	10	-0.23	0.00	-2.22	0.051
Interaction	-0.27	0.074	10	-0.43	-0.10	-3.61	0.005
univariate RM-ANOVA
(Scr EPS) - (Scr Basal)	0.15	0.040	5	0.05	0.25	3.82	0.012
(siNR4A3 EPS) - (siNR4A3 Basal)	-0.12	0.063	5	-0.28	0.04	-1.85	0.123
Interaction	-0.27	0.083	5	-0.48	-0.05	-3.22	0.023

Notes

In addition to the assumptions of the linear model outlined in the Violations chapter, the classical (“univariate model”) repeated measures ANOVA assumes sphericity, which is the equality of the variances of all pairwise differences among treatment combinations.
The univariate model of the repeated measures ANOVA is equivalent to Model exp5c_m1c. Inference (SEs, CIs, p-values) differs slightly in this here because the estimated variance for the $\texttt{donor:activity}$ random intercept of Model exp5c_m1c is zero. In cases where all variances are greater than zero and the design is balanced (no block is missing a treatment combination), the two tables would be identical.

16.8.10 “Multivariate model” repeated measures ANOVA of exp5c

Table 16.15: Planned contrasts for the linear mixed model exp5c_m1d and the multivariate model of the repeated measures ANOVA.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
exp5c_m1d
(Scr EPS) - (Scr Basal)	0.15	0.040	15	0.07	0.24	3.82	0.002
(siNR4A3 EPS) - (siNR4A3 Basal)	-0.12	0.063	15	-0.25	0.02	-1.85	0.083
Interaction	-0.27	0.083	15	-0.44	-0.09	-3.22	0.006
multivariate RM-ANOVA
(Scr EPS) - (Scr Basal)	0.15	0.040	5	0.05	0.25	3.82	0.012
(siNR4A3 EPS) - (siNR4A3 Basal)	-0.12	0.063	5	-0.28	0.04	-1.85	0.123
Interaction	-0.27	0.083	5	-0.48	-0.05	-3.22	0.023

Notes

The sphericity assumption of the repeated measures ANOVA is relaxed if the model is fit using the “multivariate model”.
The multivariate model repeated measures ANOVA is a linear model with a multivariate response and not a linear mixed model. In the multivariate model, each treatment combination is a different response variable and there is a single row for each level of the random factor ($\texttt{donor}$ in Experiment 5c). The multivariate model is a different way of handling the correlated error that occurs when conceiving of the design as univariate.
The multivariate repeated measures ANOVA can be specified using the linear mixed model exp5c_m1d. Compared to the contrasts from the multivariate model of the repeated measures ANOVA above, the SEs of the contrasts are the same but the degrees of freedom differ. Because of the increased df of the linear mixed model, the CIs are narrower and the p-value is smaller – that is the linear mixed model is less conservative than the repeated measures ANOVA. There is no correct degrees of freedom for a linear mixed model like this and emmeans outputs one way to compute these (with options for others, none of which are equivalent to those from the multivariate model RM-ANOVA).

16.8.11 Modeling $\texttt{donor}$ as a fixed effect

\[ \begin{equation} \texttt{glucose_uptake} \sim \texttt{treatment * activity + donor} \end{equation} \tag{16.5} \]

Model (16.5) (using R formula syntax) is a linear model with the block $\texttt{donor}$ added as a fixed covariate instead of a random intercept.

exp5c_m3 <- lm(glucose_uptake ~ treatment * activity + donor,
               data = exp5c)

The coefficients of the fit model are

	Estimate	Std. Error	t value	Pr(>\|t\|)	2.5 %	97.5 %
(Intercept)	1.00	0.071	14.0	0.0000	0.85	1.15
treatmentsiNR4A3	0.08	0.067	1.2	0.2453	-0.06	0.22
activityEPS	0.15	0.067	2.2	0.0402	0.01	0.29
donordonor_2	0.02	0.082	0.2	0.8444	-0.16	0.19
donordonor_3	0.16	0.082	1.9	0.0757	-0.02	0.33
donordonor_4	0.81	0.082	9.8	0.0000	0.63	0.98
donordonor_5	0.76	0.082	9.2	0.0000	0.59	0.94
donordonor_6	0.29	0.082	3.5	0.0030	0.12	0.47
treatmentsiNR4A3:activityEPS	-0.27	0.095	-2.8	0.0132	-0.47	-0.06

Notes

The coefficients include a slope for the five non-reference levels of donor. We typically don’t care about these.

Table 16.16: Planned contrasts for the linear mixed model exp5c_m1a and the fixed effect model exp5c_m3.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
exp5c_m1a
(Scr EPS) - (Scr Basal)	0.15	0.067	15	0.01	0.29	2.25	0.040
(siNR4A3 EPS) - (siNR4A3 Basal)	-0.12	0.067	15	-0.26	0.03	-1.73	0.105
Interaction	-0.27	0.095	15	-0.47	-0.06	-2.81	0.013
exp5c_m3
(Scr EPS) - (Scr Basal)	0.15	0.067	15	0.01	0.29	2.25	0.040
(siNR4A3 EPS) - (siNR4A3 Basal)	-0.12	0.067	15	-0.26	0.03	-1.73	0.105
Interaction	-0.27	0.095	15	-0.47	-0.06	-2.81	0.013

Notes

In a randomized complete block design with only 1 replicate of each treatment combination per block, like that in Experiment 5c, inference about treatment effects is exactly that same between this fixed effect model and the random intercept model exp5c_m1a.
The equivalence of inference in the treatment effect between the fixed effect and linear mixed model holds only for balanced randomized complete block designs – where all blocks contain all treatment combinations and the subsampling replicate size is the same for all treatment combinations for all blocks. This means, outside of special cases like Experiment 5c, the choice between adding a blocking variable as a random or fixed factor depends on assumptions about the model.

16.9 Example 4 – Experiments with subsampling replication (exp1g)

This example is from a design with batches (independent experiments) that contain all treatment levels of a single factor and subsampling replication. These data were used to introduce linear mixed models in Example 1. The design of the experiment is $2 \times 2$ factorial. Example 1 flattened the analysis to simplify explanation of random intercepts and random slopes. Here, the data are analyzed with a factorial model.

A GPR174–CCL21 module imparts sexual dimorphism to humoral immunity

Public source

Source figure: Fig. 1g

Source data: Source Data Fig. 1

16.9.1 Understand the data

The researchers in this paper are interested in discovering mechanisms causing the lower antibody-mediated immune response in males relative to females. The data in Fig. 1 are from a set of experiments on mice to investigate how the G-protein coupled receptor protein GPR174 regulates formation of the B-cell germinal center in secondary lymph tissue. GPR174 is a X-linked gene.

Response variable $\texttt{gc}$ – germinal center size (%). The units are the percent of cells expressing germinal center markers.

Factor 1 – $\texttt{sex}$ (“M”, “F”). Male (“M”) is the reference level.

Factor 2 – $\texttt{chromosome}$ (“Gpr174+”, “Gpr174-”). “Gpr174-” is a GPR174 knockout. The wildtype (“Gpr174+”) condition is the reference level.

Design – $2 \times 2$, that is, two crossed factors each with two levels. This results in four groups, each with a unique combination of the levels from each factor. “M Gpr174+” is the control. “M Gpr174+” is the knockout genotype in males (“knockout added”). “F Gpr174+” is the wildtype female (“X chromosome added”). “F Gpr174-” is the knockout female (“knockout and X chromosome added”.

16.9.2 Examine the data

ggplot(data = exp1g,
       aes(x = treatment,
           y = gc,
           color = experiment_id)) +
  geom_point(position = position_dodge(0.4))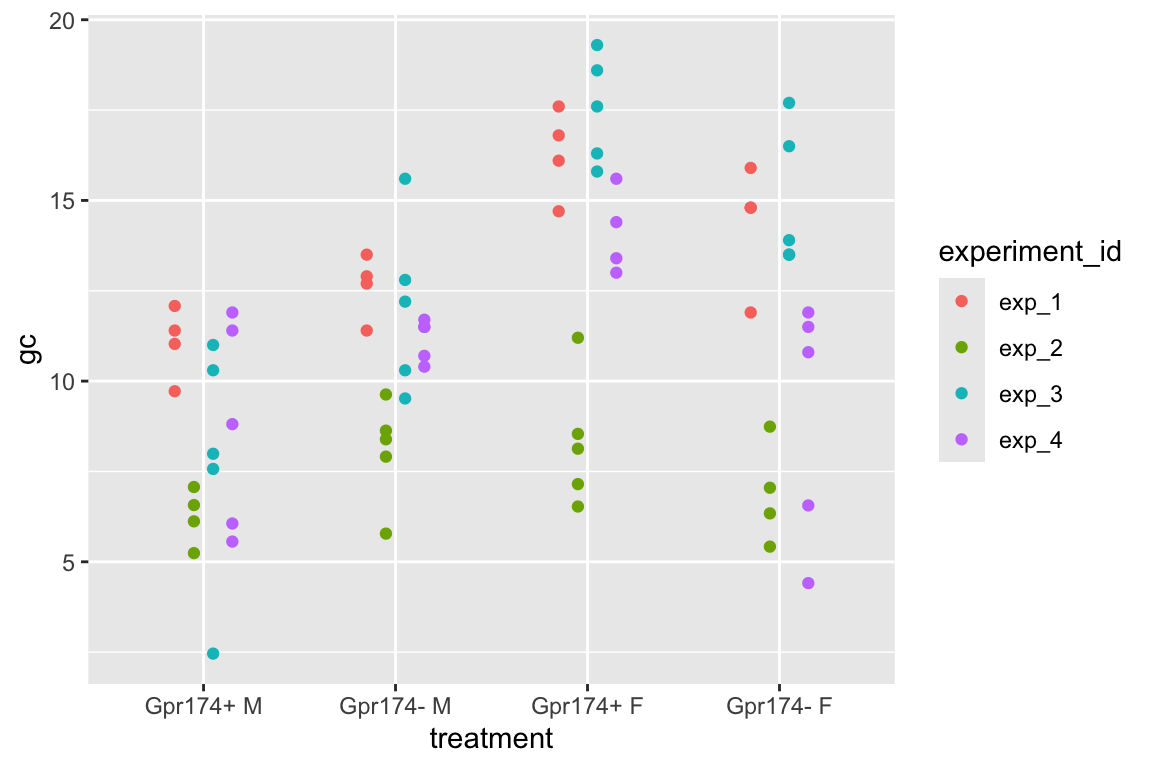

16.9.3 Fit the model

# three slope parameters
exp1g_m1a <- lmer(gc ~ genotype * sex +
                   (genotype * sex | experiment_id),
                 data = exp1g)

VarCorr(exp1g_m1a) # looks fine

##  Groups        Name                 Std.Dev. Corr                
##  experiment_id (Intercept)          1.77082                      
##                genotypeGpr174-      0.96192  -0.023              
##                sexF                 2.90154   0.459  0.878       
##                genotypeGpr174-:sexF 1.33169  -0.314 -0.625 -0.706
##  Residual                           1.93155

# one slope parameter but capturing all treatment combinations
exp1g_m1b <- lmer(gc ~ genotype * sex +
                   (treatment | experiment_id),
                 data = exp1g)

# intercept interactions
exp1g_m1c <- lmer(gc ~ genotype * sex +
                   (1 | experiment_id) +
                    (1 | experiment_id:genotype) +
                    (1 | experiment_id:sex) +
                    (1 | experiment_id:genotype:sex),
                 data = exp1g)

VarCorr(exp1g_m1c) # id:genotype is low

##  Groups                     Name        Std.Dev. 
##  experiment_id:genotype:sex (Intercept) 0.4046670
##  experiment_id:sex          (Intercept) 1.6927499
##  experiment_id:genotype     (Intercept) 0.0001216
##  experiment_id              (Intercept) 2.5487069
##  Residual                               1.9792428

# drop id:genotype which has low variance
exp1g_m1d <- lmer(gc ~ genotype * sex +
                   (1 | experiment_id) +
                    (1 | experiment_id:sex) +
                    (1 | experiment_id:sex:genotype),
                 data = exp1g)

AIC(exp1g_m1a, exp1g_m1b, exp1g_m1c, exp1g_m1d)

##           df      AIC
## exp1g_m1a 15 344.1579
## exp1g_m1b 15 344.1529
## exp1g_m1c  9 337.7602
## exp1g_m1d  8 335.7602

# go with exp1g_m1d.
exp1g_m1 <- exp1g_m1d

16.9.4 Inference from the model

exp1g_m1_coef <- coef(summary(exp1g_m1))

exp1g_m1_coef

##                       Estimate Std. Error       df   t value    Pr(>|t|)
## (Intercept)           8.435718   1.612602 4.638595  5.231123 0.004202015
## genotypeGpr174-       2.568365   0.712122 5.760582  3.606637 0.012094327
## sexF                  5.583860   1.397388 4.024010  3.995927 0.015995349
## genotypeGpr174-:sexF -5.304752   1.013552 5.918159 -5.233823 0.002033657

# order of factors reversed in specs because I want sex to be
# main x-axis variable in plot
exp1g_m1_emm <- emmeans(exp1g_m1, specs = c("sex", "genotype"))

# exp1g_m1_emm # print in console to get row numbers
# set the mean as the row number from the emmeans table
wt_m <- c(1,0,0,0)
wt_f <- c(0,1,0,0)
ko_m <- c(0,0,1,0)
ko_f <- c(0,0,0,1)

# simple effects within males and females + interaction 
# 1. (ko_m - wt_m) 
# 2. (ko_f - wt_f)

exp1g_contrasts <- list(
  "(Gpr174- M) - (Gpr174+ M)" = c(ko_m - wt_m),
  "(Gpr174- F) - (Gpr174+ F)" = c(ko_f - wt_f),
  "Interaction" = c(ko_f - wt_f) -
    c(ko_m - wt_m)
)
exp1g_m1_planned <- contrast(exp1g_m1_emm,
                       method = exp1g_contrasts,
                       adjust = "none"
) %>%
  summary(infer = TRUE)

contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
(Gpr174- M) - (Gpr174+ M)	2.57	0.714	5.784	0.81	4.33	3.60	0.012
(Gpr174- F) - (Gpr174+ F)	-2.74	0.722	6.100	-4.50	-0.98	-3.79	0.009
Interaction	-5.30	1.016	5.942	-7.80	-2.81	-5.22	0.002

Notes

The direction of the estimated effect is opposite in males and females

16.9.5 Plot the model

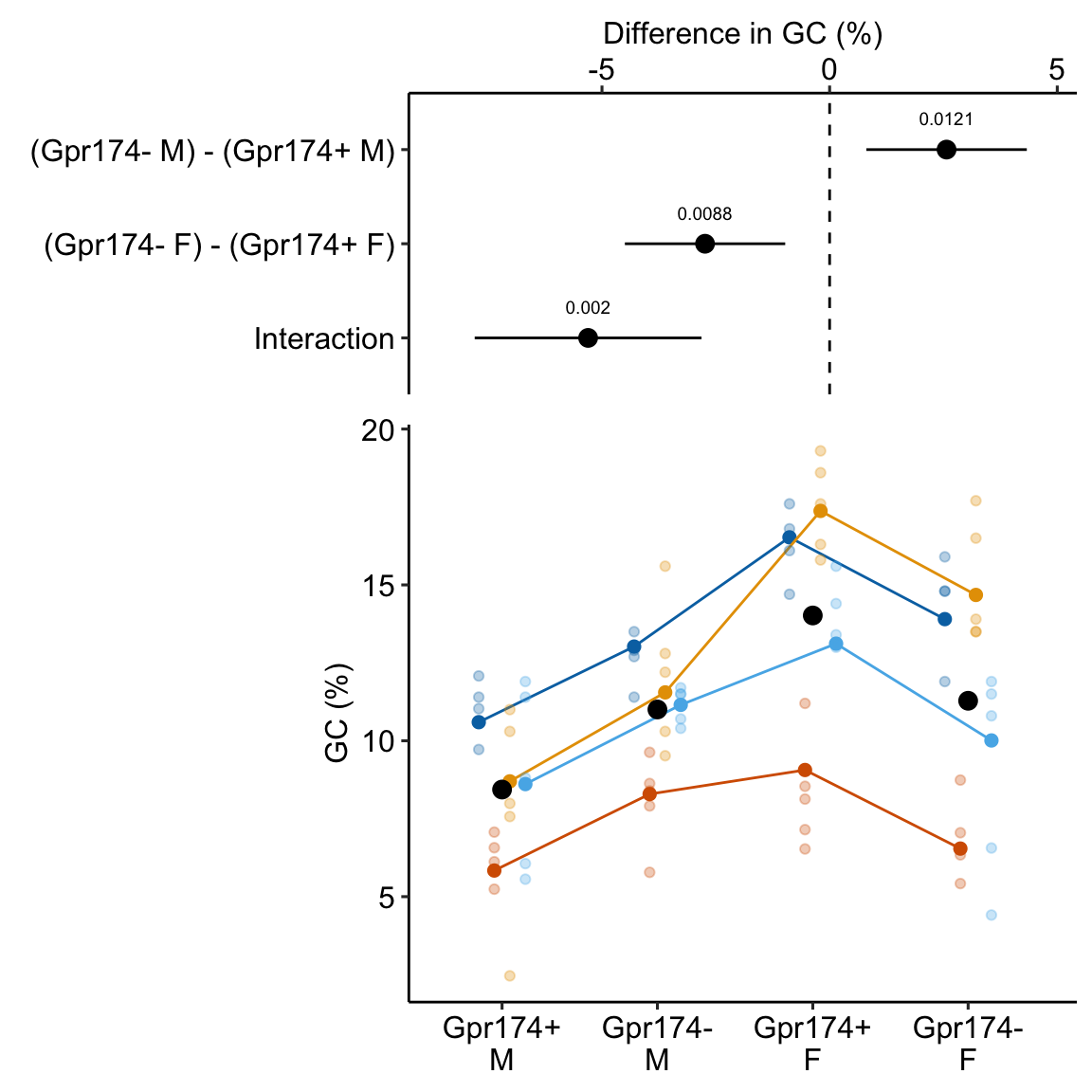
Treatment effect on germinal center (GC) formation. Small, pale, colored dots are independent experiments. Intermediate size colored dots are experiment means.

Figure 16.18: Treatment effect on germinal center (GC) formation. Small, pale, colored dots are independent experiments. Intermediate size colored dots are experiment means.

16.9.6 Alternaplot the model

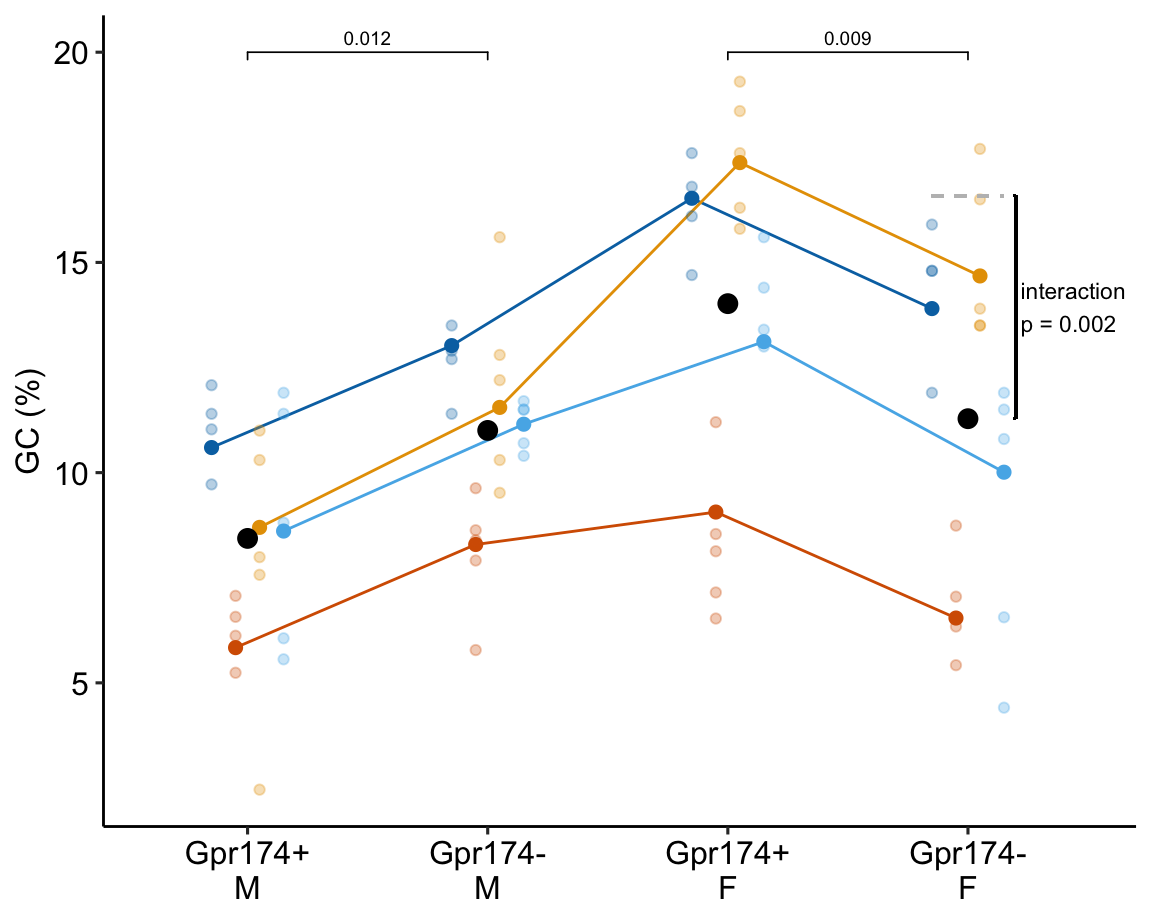
Germinal center (GC) formation in response to treatment. Small, pale, colored dots are independent experiments. Intermediate size colored dots are experiment means. Dashed gray line is expected additive mean of Gpr174- F

Figure 16.19: Germinal center (GC) formation in response to treatment. Small, pale, colored dots are independent experiments. Intermediate size colored dots are experiment means. Dashed gray line is expected additive mean of Gpr174- F

16.9.7 Understanding the alternative models

exp1g_m1a <- lmer(gc ~ genotype * sex +
                   (genotype * sex | experiment_id),
                 data = exp1g)

exp1g_m1b <- lmer(gc ~ genotype * sex +
                   (treatment | experiment_id),
                 data = exp1g)

exp1g_m1c <- lmer(gc ~ genotype * sex +
                   (1 | experiment_id) +
                    (1 | experiment_id:genotype) +
                    (1 | experiment_id:sex) +
                    (1 | experiment_id:genotype:sex),
                 data = exp1g)

exp1g_m1d <- lmer(gc ~ genotype * sex +
                   (1 | experiment_id) +
                    (1 | experiment_id:sex) +
                    (1 | experiment_id:genotype:sex),
                 data = exp1g)

Notes

All four models model the same fixed effects. The models differ only in how they model the random effects.
Model exp1g_m1a fits one random intercept, two random slopes, and one random interaction.

$\gamma_{0j}$ – a random intercept modeling batch effects of $\texttt{experiment_id}$ on the intercept
$\gamma_{1j}$ – a random slope modeling the effect of the non-reference level of “Gpr174-” on the batch effect of $\texttt{experiment_id}$. This is a $\texttt{experiment_id} \times \texttt{genotype}$ interaction.
$\gamma_{2j}$ – a random slope modeling the effect of “F” (female) on the batch effect of $\texttt{experiment_id}$. This is a $\texttt{experiment_id} \times \texttt{sex}$ interaction.
$\gamma_{3j}$ – a random slope modeling the effect of the interaction effect of “Gpr174-” and “F” on the batch effect of $\texttt{experiment_id}$. This is a $\texttt{experiment_id} \times \texttt{sex} \times \texttt{genotype}$ interaction.

Model exp1g_m1b fits one random intercept and three random slopes

$\gamma_{0j}$ – a random intercept modeling batch effects of $\texttt{experiment_id}$ on the intercept. This is modeling the same thing as $\gamma_{0j}$ in Model exp1g_m1a.
$\gamma_{1j}$ – a random slope modeling the effect of “Gpr174- M” on the batch effect of $\texttt{experiment_id}$. This is modeling the same thing as $\gamma_{1j}$ in Model exp1g_m1a.
$\gamma_{2j}$ – a random slope modeling the effect of “Gpr174+ F” on the batch effect of $\texttt{experiment_id}$. This is modeling the same thing as $\gamma_{2j}$ in Model exp1g_m1a.
$\gamma_{3j}$ – a random slope modeling the effect of “M Gpr174- F” on the batch effect of $\texttt{experiment_id}$. This is modeling the added variance accounted for by the random interaction $\gamma_{2j}$ in Model exp1g_m1a but in a different way.

Model exp1g_m1c fits four random intercepts

$\gamma_{0j}$ – a random intercept modeling batch effects of $\texttt{experiment_id}$ on the intercept. This is modeling the same thing as $\gamma_{0j}$ in Model exp1g_m1a.
$\gamma_{0jk}$ – a random intercept modeling the effects of the combination of $\texttt{experiment_id}$ and $\texttt{genotype}$. This is very similar to the variance modeled by $\gamma_{1j}$ in Model exp1g_m1a except the draws from $\gamma_{0jk}$ are independent (uncorrelated) of draws from the other random intercepts.
$\gamma_{0jl}$ – a random intercept modeling the effects of the combination of $\texttt{experiment_id}$ and $\texttt{sex}$. This is very similar to the variance modeled by $\gamma_{2j}$ in Model exp1g_m1a except the draws from $\gamma_{0jl}$ are independent (uncorrelated) of draws from the other random intercepts (review The correlation among random intercepts and slopes if this doesn’t make sense).
$\gamma_{0jkl}$ – a random intercept modeling the effects of the combination of $\texttt{experiment_id}$, $\texttt{genotype}$ and $\texttt{sex}$. This is very similar to the variance modeled by $\gamma_{3j}$ in Model exp1g_m1a except the draws from $\gamma_{0jkl}$ are independent (uncorrelated) of draws from the other random intercepts.

Model exp1g_m1d fits the same random intercepts as Model exp1g_m1c but excludes $\gamma_{0jl}$ (the random intercept for the experiment_id by genotyp combination. This was excluded because of the low variance of this component in the fit model.

16.9.8 The VarCorr matrix of models exp1g_m1a and exp1g_m1b

The random effect similarity of models exp1g_m1a and exp1g_m1b can be seen in the estimated variance components and correlations among the random effects.

Table 16.17: The Varcorr matrix. Standard deviations of random effects on the diagonal. Correlations of random effects on the off-diagonal.

exp1g_m1a
(Intercept)	1.7708
genotypeGpr174-	-0.0232	0.9619
sexF	0.4589	0.8776	2.9015
genotypeGpr174-:sexF	-0.3138	-0.6246	-0.7056	1.3317
exp1g_m1b
(Intercept)	1.7710
treatmentGpr174- M	-0.0251	0.9640
treatmentGpr174+ F	0.4585	0.8761	2.9022
treatmentGpr174- F	0.2999	0.8791	0.9384	2.9905

16.9.9 The linear mixed model has more precision and power than the fixed effect model of batch means

# means pooling model
exp1g_m2 <- lm(gc ~ sex * genotype,
                data = exp1g_means)

Table 16.18: Planned contrasts for the linear mixed model exp1g_m1 and the fixed effects model of experiment means exp1g_m2.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
exp1g_m1 (lmm)
(Gpr174- M) - (Gpr174+ M)	2.57	0.714	5.8	0.81	4.33	3.60	0.012
(Gpr174- F) - (Gpr174+ F)	-2.74	0.722	6.1	-4.50	-0.98	-3.79	0.009
Interaction	-5.30	1.016	5.9	-7.80	-2.81	-5.22	0.002
exp1g_m2 (lm means pooling)
(Gpr174- M) - (Gpr174+ M)	2.50	2.257	12.0	-2.41	7.42	1.11	0.289
(Gpr174- F) - (Gpr174+ F)	-2.73	2.257	12.0	-7.65	2.18	-1.21	0.249
Interaction	-5.24	3.192	12.0	-12.20	1.72	-1.64	0.127

Notes

A fixed effects model fit to batch-means pooled data is strongly conservative and will result in less discovery.
Means pooling does not make the data independent in a randomized complete block design. A linear mixed model of batch-means pooled data is a mixed-effect ANOVA (Next section. Also see Section 13.1.1 in the Issues chapter).

16.9.10 Fixed effect models and pseudoreplication

# complete pooling model
exp1g_m3 <- lm(gc ~ sex * genotype,
                data = exp1g)

(#tab:lmm-exp1g_m3-compare)Planned contrasts for the linear mixed model exp1g_m1 and the fixed effects model exp1g_m3 with complete pooling.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
exp1g_m1 (lmm)
(Gpr174- M) - (Gpr174+ M)	2.57	0.714	5.8	0.81	4.33	3.60	0.012
(Gpr174- F) - (Gpr174+ F)	-2.74	0.722	6.1	-4.50	-0.98	-3.79	0.009
Interaction	-5.30	1.016	5.9	-7.80	-2.81	-5.22	0.002
exp1g_m3 (lm complete pooling)
(Gpr174- M) - (Gpr174+ M)	2.44	1.111	69.0	0.22	4.65	2.20	0.032
(Gpr174- F) - (Gpr174+ F)	-2.53	1.125	69.0	-4.77	-0.28	-2.25	0.028
Interaction	-4.97	1.581	69.0	-8.12	-1.81	-3.14	0.002

Notes

Complete pooling is strongly anti-conservative and will result in increased false discovery. Complete pooling is a type of pseudoreplication – the subsamples have been analyzed as if they are independent replicates. Subsamples are not independent.
For the Experiment 1g data, the 95% confidence intervals are wider and the p-values are larger in the complete pool model exp1g_m3 compared to the linear mixed model exp1g_m1. This is an unusual result.

16.9.11 Mixed-effect ANOVA

exp1g_m1_aov <- aov_4(gc ~ sex * genotype +
                  (sex * genotype | experiment_id),
                data = exp1g)

Notes

The formula has the same format as that in Example 3 for repeated measures ANOVA on RCB designs with no subsampling. In biology, this is often called a mixed effect ANOVA with two fixed factors and one random factor.
The data are aggregated prior to fitting the model – this means the subsamples are averaged within each batch by treatment combination.
The mixed-effect ANOVA is equivalent to the linear mixed model exp1g_m1c if there are the same number of replicates in each treatment combination and the same number of subsamples in all treatment by $\texttt{experiment_id}$ combinations. The design is not balanced in this example.

(#tab:lmm-exp1g_m1_aov-pairs)Planned contrasts from mixed ANOVA compared to lmm equivalent of mixed ANOVA and lowest AIC lmm.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
exp1g_m1_aov (mixed ANOVA)
(Gpr174- M) - (Gpr174+ M)	2.50	0.599	3.000	0.60	4.41	4.18	0.025
(Gpr174- F) - (Gpr174+ F)	-2.73	0.808	3.000	-5.30	-0.16	-3.39	0.043
Interaction	-5.24	1.087	3.000	-8.70	-1.78	-4.82	0.017
exp1g_m1_c (lmm equivalent of mixed ANOVA)
(Gpr174- M) - (Gpr174+ M)	2.57	0.715	5.784	0.80	4.33	3.59	0.012
(Gpr174- F) - (Gpr174+ F)	-2.74	0.724	6.100	-4.50	-0.97	-3.78	0.009
Interaction	-5.30	1.017	2.972	-8.56	-2.05	-5.21	0.014
exp1g_md (lmm with min AIC)
(Gpr174- M) - (Gpr174+ M)	2.57	0.714	5.784	0.81	4.33	3.60	0.012
(Gpr174- F) - (Gpr174+ F)	-2.74	0.722	6.100	-4.50	-0.98	-3.79	0.009
Interaction	-5.30	1.016	5.942	-7.80	-2.81	-5.22	0.002

16.10 Statistical models for experimental designs

16.10.1 Models for Completely Randomized Designs (CRD)

lm0 <- lm(y ~ treatment,
             data = figx)

16.10.2 Models for batched data (CRDS, RCBD, RSPD, GRCBD, NRCBD)

16.10.2.1 Linear models

16.10.2.1.1 fixed effect model

lm1 <- lm(y ~ treatment + block,
             data = figx)

16.10.2.1.2 linear model of batch means

figx_means <- figx[, .(y = mean(y)),
               by = .(treatment, batch)]
lm2 <- lm(y ~ treatment,
             data = figx_means)

16.10.2.2 linear mixed models (“random effects” models)

16.10.2.2.1 Random intercept model

lmm1 <- lmer(y ~ treatment + (1 | block),
              data = figx)

16.10.2.2.2 lmm for correlated error

lmm2 <- lme(y ~ treatment,
             random = ~1 | block,
             correlation = corSymm(form = ~ 1 | block),
             weights = varIdent(form = ~ 1 | treatment),
             data = figx)

16.10.2.2.3 random intercept and slope model

lmm3 <-  lmer(y ~ treatment + (treatment | block),
               data = figx)

16.10.2.2.4 random interaction intercept model

lmm4 <-  lmer(y ~ treatment + (1 | block) + (1 | block:treatment),
               data = figx)

16.10.2.2.5 random interaction model with subsampling

lmm5 <-  lmer(y ~ treatment + (1 | block) + (1 | block:treatment) + (1 | block:treatment:replicate),
               data = figx)

16.10.2.2.6 CRD split plot model

# tr1 is the main plot
# tr2 is the subplot
# main_plot is tr1:rep, where rep is the rep id
lmm6 <-  lmer(y ~ tr1 * tr2 + (1 | main_plot),
               data = figx)

16.10.2.2.7 RCBD split plot model

# tr1 is the main plot
# tr2 is the subplot
# main_plot is tr1:block
lmm7 <-  lmer(y ~ tr1 * tr2 + (1 | block) + (1 | block:tr1),
               data = figx)

lmm7 <-  lmer(y ~ tr1 * tr2 + block + (1 | block:tr1),
               data = figx)
# the two versions are numerically equivalent

16.10.2.3 ANOVA models (“mixed models”, “repeated measures ANOVA”)

16.10.2.3.1 Multivariate repeated measures ANOVA

aov1 <- aov_4(y ~ treatment + (treatment | block),
             data = figx)

16.10.2.3.2 Univariate repeated measures ANOVA

aov2 <- aov_4(y ~ treatment + (treatment | block),
           include_aov = TRUE,
             data = figx)

16.10.2.3.3 Pairwise paired, t-tests

pptt <- pairwise_t_tests(y_col = "y",
                         g_col = "treatment",
                         id_col = "block",
                         data = figx)

16.11 Which model and why?

16.11.1 CRD

No batch to model!

16.11.2 CRDS

lmm1 – random intercept model
lm2 – linear model of batch means

Notes

These are numerically equivalent and should result in same estimates, SE, CIs, and p-values
These are equivalent to a Nested t-test or Nested ANOVA

16.11.3 RCBD

Reasonable models:

lmm1 – random intercept model
lmm2 – lmm for correlated error
lm1 – fixed effect model
aov1 – multivariate RM-ANOVA
aov2 – univariate RM-ANOVA
pptt – pairwise, paired t-test

(Cannot use lmm3 or lmm4 because there is no replication of each block:treatment combination.)

Assumptions:

lmm1, lm1, and aov2 assume
- compound symmetry.
- sphericity.
lmm2, aov1, and pptt do not assume compound symmetry and sphericity.

Notes:

lmm1 is the standard. If the number of treatments = 2, then lmm1 is eqivalent with a paired t-test.
If the design is balanced (all blocks have a single value for both treatments) AND the number of treatments = 2 then all six methods are numerically equivalent.
If the design is balanced AND the number of treatments > 2, then
- lmm1, lm1, and aov2 are numerically equivalent
- lmm2, aov1, pptt result in the same estimates and SE but lmm2 has more df, so the CIs, and p-values of lmm2 are less conservative.
If the number of treatments = 2 AND the design is not balanced (at least one block is missing value for one treatment level) then the linear models (lm1, aov1, aov2, pptt) are equivalent but the linear mixed models (lmm1, lmm2) differ from each other and from the linear models.
If a treatment within a block is missing, the whole block is deleted in the RM-ANOVA models. This reduces power (the loss of power depends partly on the number of missing values).
If a treatment within a block is missing, the block is deleted only in the comparisons including the missing treatment in the pairwise, paired t-tests. This makes pptt more powerful than aov1.
the lmm models are very flexible – covariates can be added or these can be used as generalized lmms for non-normal distributions.
the lmm models and especially lmm2 sometimes (often?) fail to converge, especially with small samples (small number of blocks) or if the among-block component of variance is small.

Performance:

Table 16.19: Type I error rate the RCBD statistical models under different levels of correlation structure among the observations. The Cor Error column is the average correlated error of the residuals fit by a simple linear model y ~ treatment. Model abbreviations as in text.
Contrast	Cor Error	lm0	lm1	aov1	aov2	pptt	lmm2
sim 1 - high correlated error
Cn, Tr1	0.299	0.047	0.110	0.058	0.110	0.058	0.068
Cn, Tr2	0.412	0.027	0.090	0.052	0.090	0.052	0.070
Tr1, Tr2	0.662	0.000	0.005	0.063	0.005	0.063	0.070
sim 2 - low correlated error
Cn, Tr1	0.165	0.044	0.072	0.055	0.072	0.055	0.063
Cn, Tr2	0.164	0.051	0.077	0.060	0.077	0.060	0.076
Tr1, Tr2	0.238	0.016	0.028	0.062	0.028	0.062	0.079
sim 3 - equal correlated error
Cn, Tr1	0.771	0.001	0.057	0.058	0.057	0.058	0.069
Cn, Tr2	0.773	0.001	0.049	0.056	0.049	0.056	0.067
Tr1, Tr2	0.769	0.002	0.056	0.056	0.056	0.056	0.074
sim 4 - zero correlated error
Cn, Tr1	0.025	0.050	0.047	0.042	0.047	0.042	0.061
Cn, Tr2	0.010	0.054	0.054	0.046	0.054	0.046	0.061
Tr1, Tr2	0.000	0.056	0.060	0.053	0.060	0.053	0.076

aov1, pptt, and lmm2 have well-behaved type I error rates (lmm2 is a little anti-conservative) regardless of correlation structure – False discoveries should be well controlled.
lm1, lmm1, and aov2 have poorly-behaved type I error rates when there is a block:treatment interaction (sim 1 and 2), resulting in heterogenous correlation structure (remember that this is moot when there are only two treatment levels) – this consequence is small when the block and block:treatment variance is small (small correlations in residuals). When there is block:treatment interaction, these models are conservative in contrasts associated with large residual correlation, resulting in low power, and anti-conservative in contrasts associated with small residual correlations. resulting in high false discovery rates.

Best Practices:

If the number of treatments = 2 and
- the design is balanced: it doesn’t matter which method you use.
- the design is not balanced: use lmm1 or lmm2
If the number of treatments > 2 and
- the design is balanced: use aov1/pptt (these are numerically equivalent). lmm1 is the standard but it assumes equal correlated error among treatment levels and equal standard errors among contrasts. lmm2 explicitly models heterogeneity of correlations and variances but 1) the model often fails and 2) has slightly anti-conservative Type I error.
- the design is not balanced: lmm2 is attractive if the model runs. pptt is attractive if there are few missing values.
If there are covariates, then start with lmm2. Use lmeControl if lmm2 fails. If this fails, use pairwise lmm1, which is the same as pairwise t-tests but allows covariates to be added to the model. Note that the covariate will be modeled independently in each pair, which effectively models the consequence of a treatment:covariate interaction.

16.11.4 RSPD

Reasonable models:

lmm4 – random interaction intercept model

Assumptions:

Notes:

Performance:

Table 16.20: Type I error rate for the RSPD statistical models under different models of random variance. The design is 2 (main plot: WT, KO) x 3 (subplot: Cn, Tr1, Tr2) with ten blocks. All four simulations have a component of variance due to block. Sim 1 includes a block:main plot component, Sim 2 includes a block:sub plot component, Sim 3 includes both block:main and block:sub components. Type I error rates for the 9 simple effect contrasts were averaged within the two sets: contrast = main is the aggregate of the single main plot contrast (KO - WT) at each level of the subplot factor. contrast = sub is the aggregate of the three subplot contrasts (Tr1 - Cn, Tr2 - Cn, Tr2 - Tr1) at each level of the main plot factor. The Cor Error column is the average correlated error of the residuals fit by a simple linear model y ~ treatment. Model abbreviations as in text.
sim_id	sig_block	sig_ss	sig_main	sig_sub	contrast	r	lm0	lm1	lmm1	lmm3	lmm4	lmm5	lmm6
sim 1 - block:main plot
1	0.8	0.5	0.6	0.0	main	0.494	0.010	0.199	0.087	0.051	0.052	0.083	0.054
1	0.8	0.5	0.6	0.0	sub	0.783	0.000	0.052	0.011	0.052	0.052	0.011	0.052
sim 2 - block:sub plot
2	0.8	0.5	0.0	0.6	main	0.782	0.000	0.002	0.003	0.002	0.003	0.042	0.041
2	0.8	0.5	0.0	0.6	sub	0.497	0.008	0.053	0.066	0.068	0.065	0.050	0.053
sim 3 - block:main + block:sub
3	0.8	0.5	0.6	0.4	main	0.549	0.007	0.111	0.062	0.038	0.039	0.068	0.054
3	0.8	0.5	0.6	0.4	sub	0.689	0.001	0.056	0.026	0.057	0.056	0.024	0.054
sim 4 - block only
4	0.8	0.5	0.0	0.0	main	0.707	0.002	0.049	0.049	0.044	0.045	0.056	0.054
4	0.8	0.5	0.0	0.0	sub	0.704	0.002	0.057	0.055	0.061	0.060	0.052	0.059

16.11.5 RCBDS

lmm3 – random intercept and slopes model
lmm4 – random interaction intercept model
lmm1 – random intercept model on batch means
lmm2 – lmm for correlated error on batch means
aov1 – multivariate RM-ANOVA
aov2 – univariate RM-ANOVA
pptt – pairwise, paired t-test

Notes

lmm3 is the “maximal model” – it fits the most parameters and has the fewest assumptions. lmm1 on the full data is the minimal model. I’m not recommending this at all as this is pseudoreplication and will result in very anti-conservative inference. lmm4 is less conservative than lmm3 (and makes more assumptions).
lmm1 and lmm2 here are the models for RCBD designs but using the aggregated data - that is the subsampled replicates within a batch (block:treatment combination) are averaged.
If design is balanced
- lmm3 and aov1 result in same estimates, SE, CIs, and p-values
- lmm4, lmm1, and aov2 result in same estimates, SE, CIs, and p-values
- lmm2 has same estimates and SE as lmm3/aov1 but more df so less conservative
If a treatment within a block is missing, the whole block is deleted in the RM-ANOVA models. This reduces power
the lmm models are very flexible – covariates can be added or these can be used as generalized lmms for non-normal distributions.
the lmm models, and especially lmm2 and lmm3, sometimes (often?) fail to converge, especially with small samples (small number of blocks) or if within block correlation is small
lmm1, lmm4, and aov2 will be less conservative (more power but at higher type I error/false positive rate)

Best practices

If balanced and no covariates then use lmm3/lmm2/aov1 if discovery is expensive (want to avoid false positives) or lmm4/aov2/lmm1 if discovery is cheap (can afford false positives). lmm2 is less conservative than lmm3/aov1. Use lmm3 if interested in the variance at different levels and/or covariance structure.
If unbalanced, or if there are covariates, then start with lmm3 or lmm2. Use lmeControl if lmm2 fails. If these fail, go to 1.

16.11.6 GRCBD

lmm3 – random intercept and slopes model
lmm4 – random interaction intercept model
lmm1 – random intercept model on block:treatment means
lmm2 – lmm for correlated error on block:treatment means
aov1 – multivariate RM-ANOVA
aov2 – univariate RM-ANOVA
lm1 – fixed effect model on all data
pptt – pairwise, paired t-test on block:treatment means

16.11.7 GRCBDS

lmm3 – random intercept and slopes model
lmm4 – random interaction intercept model
lmm1 – random intercept model on block:treatment means
lmm2 – lmm for correlated error on block:treatment means
aov1 – multivariate RM-ANOVA
aov2 – univariate RM-ANOVA
lm1 – fixed effect model on all block:treatment:rep means
pptt – pairwise, paired t-test on block:treatment:rep means

16.12 Working in R

16.12.1 Plotting models fit to batched data

16.12.1.1 Models without subsampling - Experiment 6g

Data wrangling necessary for plot:

# convert contrast table to a data.table
exp6g_m1_planned_dt <- data.table(exp6g_m1_planned)

# create a pretty p-value column
exp6g_m1_planned_dt[, pretty_p := pvalString(p.value)]

# add group1 and group2 columns to exp1g_m1_planned
exp6g_m1_planned_dt[, group1 := c("Saline", "CNO", "Post_CNO")]
exp6g_m1_planned_dt[, group2 := c("Lesion", "Saline", "CNO")]

Experiments are colored:

gg1 <- ggplot(data = exp6g,
              aes(x = treatment,
                  y = touch,
                  color = mouse_id)) +
  geom_point(position = position_dodge(width = 0.2)) +
  geom_line(aes(group = mouse_id),
            position = position_dodge(width = 0.2),
            color = "gray80") +
  geom_point(data = summary(exp6g_m1_emm),
             aes(y = emmean),
             color = "black",
             size = 3) +
  geom_errorbar(data = summary(exp6g_m1_emm),
             aes(y = emmean,
                 ymin = lower.CL,
                 ymax = upper.CL),
             color = "black",
             width = .05) +

  # pvalue brackets
  stat_pvalue_manual(exp6g_m1_planned_dt,
                     label = "pretty_p",
                     y.position = c(99,97,95),
                     size = 2.5,
                     tip.length = 0.01) +

  ylab("Percent ipsilateral touch") +
  scale_color_manual(values = pal_okabe_ito_blue) +
  theme_pubr() +
  theme(
    axis.title.x = element_blank(), # no x-axis title
    legend.position = "none"
  ) + 
  NULL

Treatments are colored:

gg2 <- ggplot(data = exp6g,
              aes(x = treatment,
                  y = touch)) +
  geom_point(aes(group = mouse_id),
             position = position_dodge(width = 0.2),
             color = "gray") +
  geom_line(aes(group = mouse_id),
            position = position_dodge(width = 0.2),
            color = "gray80") +
  geom_point(data = summary(exp6g_m1_emm),
             aes(y = emmean,
             color = treatment),
             size = 3) +
  geom_errorbar(data = summary(exp6g_m1_emm),
             aes(y = emmean,
                 ymin = lower.CL,
                 ymax = upper.CL,
             color = treatment),
             width = .05) +
  
  # pvalue brackets
  stat_pvalue_manual(exp6g_m1_planned_dt,
                     label = "pretty_p",
                     y.position = c(99,97,95),
                     size = 2.5,
                     tip.length = 0.01) +

  ylab("Percent ipsilateral touch") +
  scale_color_manual(values = pal_okabe_ito_blue) +
  theme_pubr() +
  theme(
    axis.title.x = element_blank(), # no x-axis title
    legend.position = "none"
  ) + 
  NULL

#gg2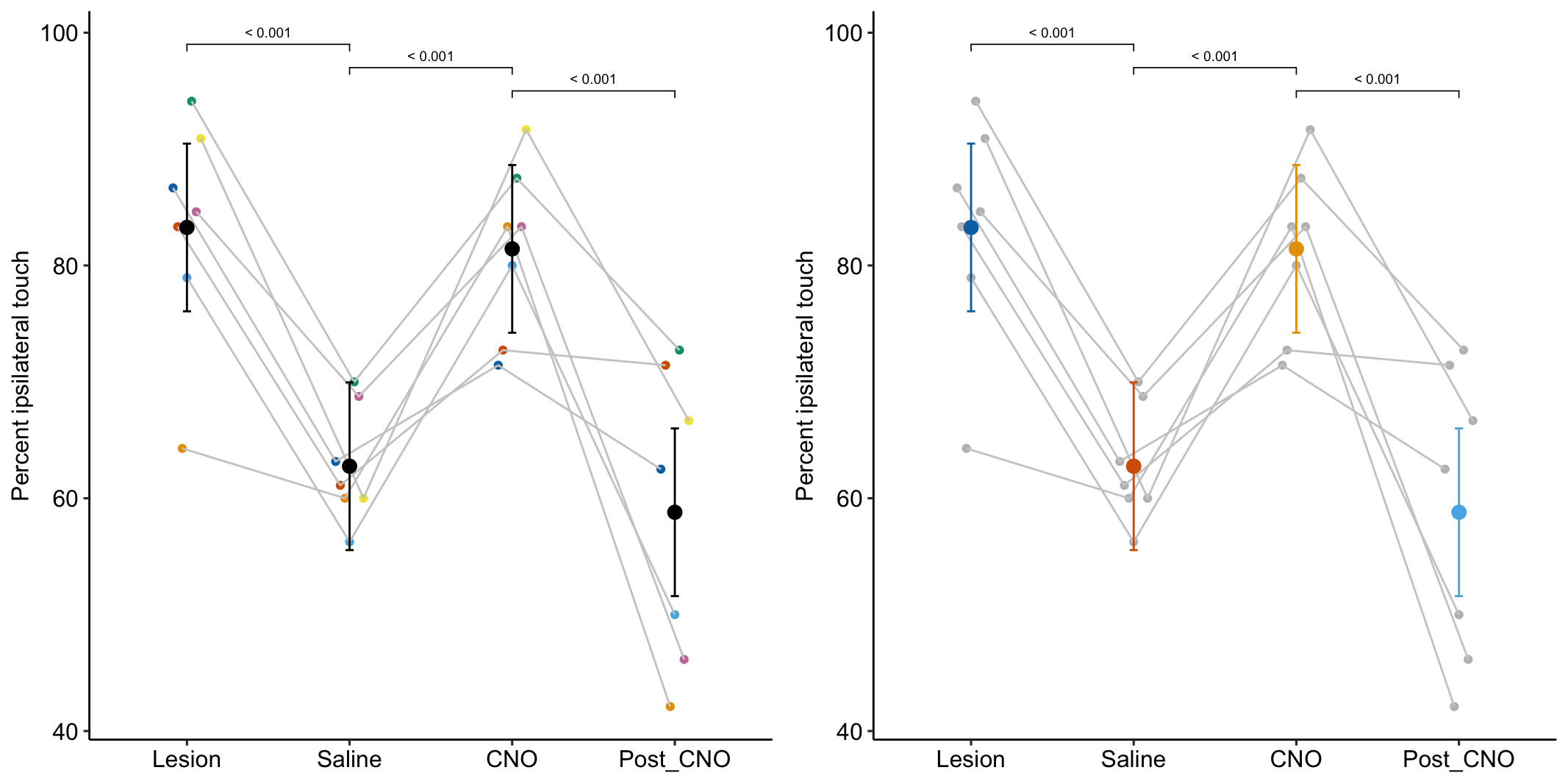

16.12.1.2 Models with subsampling - Experiment 1g

Data wrangling necessary for plot:

# add treatment column to emmeans table
exp1g_m1_emm_dt <- summary(exp1g_m1_emm) %>%
  data.table
exp1g_m1_emm_dt[, treatment := paste(genotype, sex)]
exp1g_m1_emm_dt[, treatment := factor(treatment,
                                      levels = levels(exp1g$treatment))]

# create table of means for each treatment * experiment_id combination
exp1g[, group_mean := predict(exp1g_m1)]
exp1g_m1_emm2 <- exp1g[, .(group_mean = mean(group_mean)),
                       by = .(treatment, experiment_id)]

# add group1 and group2 columns to exp1g_m1_planned
exp1g_m1_planned_dt <- data.table(exp1g_m1_planned)
exp1g_m1_planned_dt[, pretty_p := pvalString(p.value)]
exp1g_m1_planned_dt[, group1 := c("Gpr174- M", "Gpr174- F", "")]
exp1g_m1_planned_dt[, group2 := c("Gpr174+ M", "Gpr174+ F", "")]

# get coefficients of model
b <- exp1g_m1_coef[, "Estimate"]

# get interaction p
p_ixn <- exp1g_m1_planned_dt[contrast == "Interaction", pretty_p]

exp1g_plot_a <- ggplot(data = exp1g,
              aes(x = treatment,
                  y = gc,
                  color = experiment_id)) +
  # modeled experiment by treatment means
  geom_point(data = exp1g_m1_emm2,
            aes(y = group_mean,
                color = experiment_id),
            position = position_dodge(width = 0.4),
            alpha = 1,
            size = 2) +
  geom_line(data = exp1g_m1_emm2,
            aes(y = group_mean,
                group = experiment_id,
                color = experiment_id),
            position = position_dodge(width = 0.4)) +
  
  # raw data
  geom_point(position = position_dodge(width = 0.4),
             alpha = 0.3
  ) +
  
  # modeled treatment means
  geom_point(data = exp1g_m1_emm_dt,
             aes(y = emmean),
             color = "black",
             size = 3) +
  # geom_errorbar(data = exp1g_m1_emm_dt,
  #            aes(y = emmean,
  #                ymin = lower.CL,
  #                ymax = upper.CL),
  #             color = "black",
  #           width = .05) +
  
  # pvalue brackets
  stat_pvalue_manual(exp1g_m1_planned_dt[1:2],
                     label = "pretty_p",
                     y.position = c(20,20),
                     size = 2.5,
                     tip.length = 0.01) +
  
  # additive line + interaction p bracket
  geom_segment(x = 3.85,
               y = b[1] + b[2] + b[3],
               xend = 4.15,
               yend = b[1] + b[2] + b[3],
               linetype = "dashed",
               color = "gray") +
  geom_bracket(
    x = 4.2,
    y = b[1] + b[2] + b[3],
    yend = b[1] + b[2] + b[3] + b[4],
    label = paste0("interaction\np = ", p_ixn),
    text.size = 3,
    text.hjust = 0,
    color = "black") +
  
  ylab("GC (%)") +
  scale_color_manual(values = pal_okabe_ito_blue) +
  theme_pubr() +
  coord_cartesian(xlim = c(1, 4.1)) +
  theme(
    axis.title.x = element_blank(), # no x-axis title
    legend.position = "none"
  ) + 
  NULL
  
exp1g_plot_a <- factor_wrap(exp1g_plot_a)

#exp1g_plot_a

# get coefficients of model
b <- exp1g_m1_coef[, "Estimate"]

# get interaction p
p_ixn <- exp1g_m1_planned_dt[contrast == "Interaction", pretty_p]

dodge_width = 0.6
exp1g_plot_b <- ggplot(data = exp1g,
              aes(x = treatment,
                  y = gc,
                  group = experiment_id)) +
  # modeled experiment by treatment means
  geom_point(data = exp1g_m1_emm2,
            aes(y = group_mean,
                color = experiment_id),
            position = position_dodge(width = dodge_width),
            alpha = 1,
            size = 2) +
  geom_line(data = exp1g_m1_emm2,
            aes(y = group_mean,
                group = experiment_id,
                color = experiment_id),
            position = position_dodge(width = dodge_width)) +
  
  # raw data
  geom_point(position = position_dodge(width = dodge_width),
             color = "gray80"
  ) +
  
  # modeled treatment means
  geom_point(data = exp1g_m1_emm_dt,
             aes(y = emmean),
             color = "black",
             size = 3) +
  # geom_errorbar(data = exp1g_m1_emm_dt,
  #            aes(y = emmean,
  #                ymin = lower.CL,
  #                ymax = upper.CL),
  #             color = "black",
  #           width = .05) +
  
  # pvalue brackets
  stat_pvalue_manual(exp1g_m1_planned_dt[1:2],
                     label = "pretty_p",
                     y.position = c(20,20),
                     size = 2.5,
                     tip.length = 0.01) +
  
  # additive line + interaction p bracket
  geom_segment(x = 4 - dodge_width/2,
               y = b[1] + b[2] + b[3],
               xend = 4 + dodge_width/2,
               yend = b[1] + b[2] + b[3],
               linetype = "dashed",
               color = "gray") +
  geom_bracket(
    x = 4 + dodge_width/1.9,
    y = b[1] + b[2] + b[3],
    yend = b[1] + b[2] + b[3] + b[4],
    label = paste0("interaction\np = ", p_ixn),
    text.size = 3,
    text.hjust = 0,
    color = "black") +
  
  ylab("GC (%)") +
  scale_color_manual(values = pal_okabe_ito_blue) +
  theme_pubr() +
  coord_cartesian(xlim = c(1, 4.2)) +
  theme(
    axis.title.x = element_blank(), # no x-axis title
    legend.position = "none"
  ) + 
  NULL
  
exp1g_plot_b <- factor_wrap(exp1g_plot_b)

# exp1g_plot_b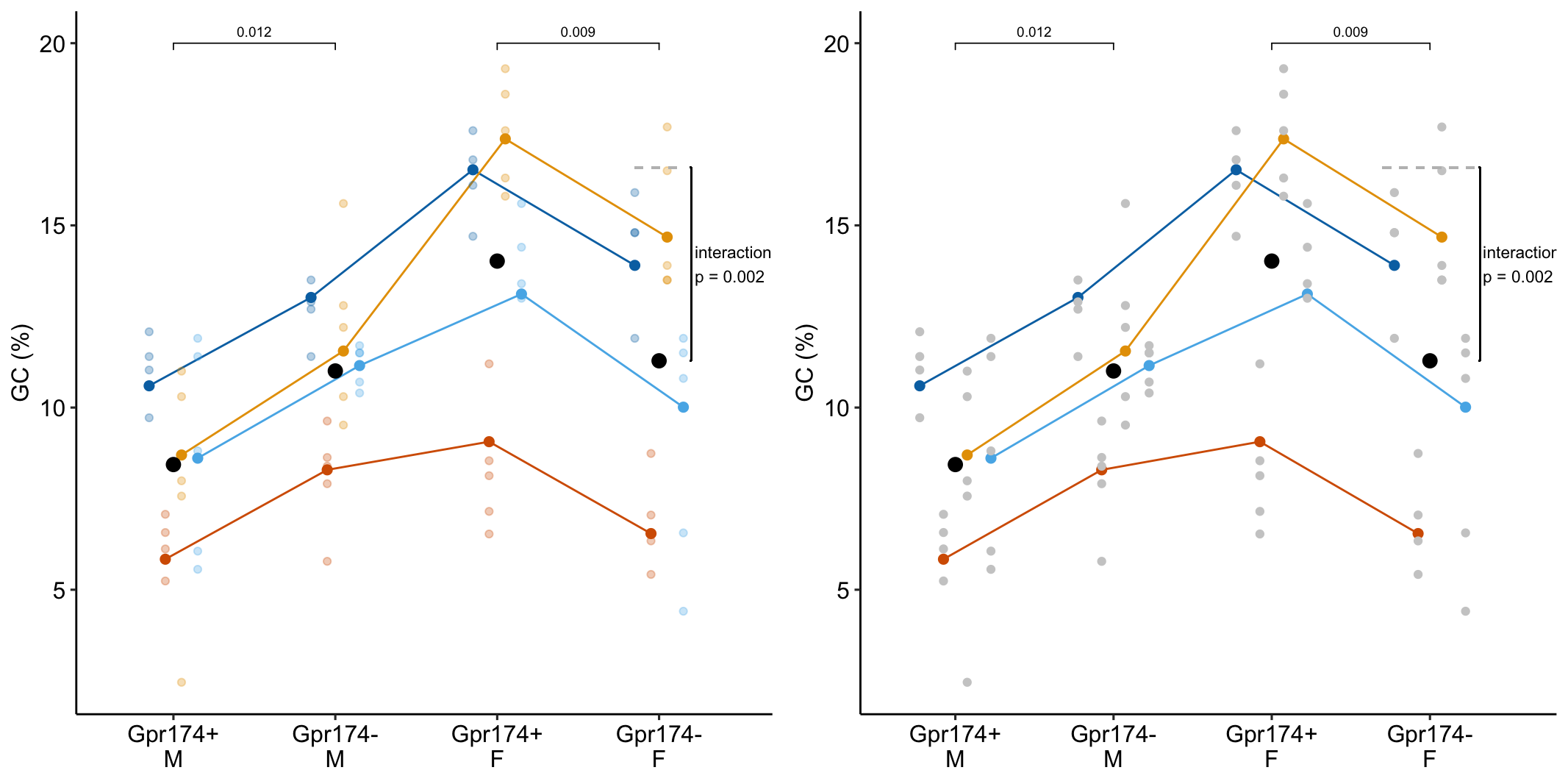

16.12.2 Repeated measures ANOVA (randomized complete block with no subsampling)

# this is the rm-ANOVA
m1 <- aov_4(glucose_uptake ~ treatment * activity +
              (treatment * activity | donor),
            data = exp5c)

# lmm equivalent

m2 <- lmer(glucose_uptake ~ treatment * activity +
         (1 | donor) +
         (1 | donor:treatment) +
         (1 | donor:activity),
       data = exp5c)

# random intercept and slope model that is *not* equivalent
# this isn't solvable because there is no subsampling

m3 <- lmer(glucose_uptake ~ treatment * activity +
              (treatment * activity | donor),
            data = exp5c)

Notes

afex computes the repeated measures anova model using both aov (classical univariate repeated measures ANOVA) and using lm with multiple response variables (the multivariate repeated measures ANOVA). As of this writing, the output from aov is the default.
Given only one measure for each donor within a $\texttt{treatment} \times \texttt{activity}$ combination, the linear mixed model m2 is equivalent to the univariate repeated measures model m1.
The model formula in m1 looks like that in the linear mixed model m3 but the two models are not equivalent.

16.12.2.1 univariate vs. multivariate repeated measures ANOVA

Use the multivariate model unless you want to replicate the result of someone who used a univariate model. By default, aov_4 computes only the multivariate model (prior to version xxx, the default was to compute both models).

# default mode -- should be multivariate
exp5c_aov <- aov_4(glucose_uptake ~ treatment * activity +
                    (treatment * activity | donor),
                  data = exp5c)

# force aov_4 to compute univariate model
exp5c_aov1 <- aov_4(glucose_uptake ~ treatment * activity +
                    (treatment * activity | donor),
                  data = exp5c,
                  include_aov = TRUE)

# explicitly exclude the univariate model
exp5c_aov2 <- aov_4(glucose_uptake ~ treatment * activity +
                    (treatment * activity | donor),
                  data = exp5c,
                  include_aov = FALSE)

Notes

The include_aov = TRUE argument forces output from aov_4 to include the univariate model.

contrasts from multivariate model

# These three should give equivalent results

# exp5c_aov was fit with the default -- multivariate model only
emmeans(exp5c_aov,
        specs = c("treatment", "activity")) %>%
  contrast(method = "revpairwise",
           simple = "each",
           combine = TRUE,
           adjust = "none")

##  activity treatment contrast      estimate     SE df t.ratio p.value
##  Basal    .         siNR4A3 - Scr   0.0813 0.1012  5   0.804  0.4581
##  EPS      .         siNR4A3 - Scr  -0.1858 0.0359  5  -5.180  0.0035
##  .        Scr       EPS - Basal     0.1510 0.0395  5   3.821  0.0124
##  .        siNR4A3   EPS - Basal    -0.1161 0.0626  5  -1.855  0.1228

# exp5c_aov included the univariate model but the default is still the multivariate model
emmeans(exp5c_aov1,
        specs = c("treatment", "activity")) %>%
  contrast(method = "revpairwise",
           simple = "each",
           combine = TRUE,
           adjust = "none")

##  activity treatment contrast      estimate     SE df t.ratio p.value
##  Basal    .         siNR4A3 - Scr   0.0813 0.1012  5   0.804  0.4581
##  EPS      .         siNR4A3 - Scr  -0.1858 0.0359  5  -5.180  0.0035
##  .        Scr       EPS - Basal     0.1510 0.0395  5   3.821  0.0124
##  .        siNR4A3   EPS - Basal    -0.1161 0.0626  5  -1.855  0.1228

# passing `model = "multivariate"` makes the model choice transparent
emmeans(exp5c_aov1,
        specs = c("treatment", "activity"),
        model = "multivariate") %>%
  contrast(method = "revpairwise",
           simple = "each",
           combine = TRUE,
           adjust = "none")

##  activity treatment contrast      estimate     SE df t.ratio p.value
##  Basal    .         siNR4A3 - Scr   0.0813 0.1012  5   0.804  0.4581
##  EPS      .         siNR4A3 - Scr  -0.1858 0.0359  5  -5.180  0.0035
##  .        Scr       EPS - Basal     0.1510 0.0395  5   3.821  0.0124
##  .        siNR4A3   EPS - Basal    -0.1161 0.0626  5  -1.855  0.1228

Notes

If our rmANOVA model is fit with the default specification (exp5c_aov1), we can get the multivariate output using the model = "multivariate" argument within emmeans (not the contrast function!). Or, if our fit excluded the univariate model (exp5c_aov2), then we don’t need the model argument.

contrasts from univariate model

# get the univariate model results using $aov
emmeans(exp5c_aov1$aov, specs = c("treatment", "activity")) %>%
  contrast(method = "revpairwise",
           simple = "each",
           combine = TRUE,
           adjust = "none")

##  activity treatment contrast      estimate     SE   df t.ratio p.value
##  Basal    .         siNR4A3 - Scr   0.0813 0.0759 8.60   1.071  0.3132
##  EPS      .         siNR4A3 - Scr  -0.1858 0.0759 8.60  -2.448  0.0380
##  .        Scr       EPS - Basal     0.1510 0.0524 9.39   2.884  0.0173
##  .        siNR4A3   EPS - Basal    -0.1161 0.0524 9.39  -2.218  0.0525

Notes

Passing exp5c_aov1 to emmeans will return the contrasts from the multivariate. change this to the univariate model by passing exp5c_aov1$aov.

16.12.2.2 The ANOVA table

nice(exp5c_aov1, correction = "GG")

## Anova Table (Type 3 tests)
## 
## Response: glucose_uptake
##               Effect   df  MSE       F   ges p.value
## 1          treatment 1, 5 0.02    0.68  .006     .45
## 2           activity 1, 5 0.01    0.30 .0006     .61
## 3 treatment:activity 1, 5 0.01 10.37 *   .04     .02
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1

nice(exp5c_aov1, correction = "none")

## Anova Table (Type 3 tests)
## 
## Response: glucose_uptake
##               Effect   df  MSE       F   ges p.value
## 1          treatment 1, 5 0.02    0.68  .006     .45
## 2           activity 1, 5 0.01    0.30 .0006     .61
## 3 treatment:activity 1, 5 0.01 10.37 *   .04     .02
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1

Notes

The Greenhouse-Geiger (“GG”) correction is the default. While the correction = "GG" argument is not needed, it makes the script more transparent.
For these data the Greenhouse-Geiger correction doesn’t make a difference in the table.

16.13 Hidden code

16.13.1 Import exp5c

data_from <- "Transcriptomic profiling of skeletal muscle adaptations to exercise and inactivity"
file_name <- "41467_2019_13869_MOESM6_ESM.xlsx"
file_path <- here(data_folder, data_from, file_name)

exp5c_wide <- read_excel(file_path,
                         sheet = "Fig5c",
                         range = "A2:M3",
                         col_names = FALSE) %>%
  data.table() %>%
  transpose(make.names = 1)

activity_levels <- c("Basal", "EPS")
treatment_levels <- names(exp5c_wide)
exp5c_wide[, activity := rep(activity_levels, each = 6)]
exp5c_wide[, activity := factor(activity, levels = activity_levels)]

exp5c <- melt(exp5c_wide,
              id.vars = "activity",
              variable.name = "treatment",
              value.name = "glucose_uptake")
exp5c[, treatment := factor(treatment, levels = treatment_levels)]

exp5c[, donor := rep(paste0("donor_", 1:6), 4)]

16.13.2 Import exp1g

data_from <- "A GPR174–CCL21 module imparts sexual dimorphism to humoral immunity"
file_name <- "41586_2019_1873_MOESM3_ESM.xlsx"
file_path <- here(data_folder, data_from, file_name)

exp1g_wide <- read_excel(file_path,
                         sheet = "Fig 1g",
                         range = "B4:E25",
                         col_types = c("numeric"),
                         col_names = FALSE) %>%
  data.table()

genotype_levels <- c("Gpr174+", "Gpr174-")
sex_levels <- c("M", "F")
g.by.s_levels <- do.call(paste, expand.grid(genotype_levels, sex_levels))
colnames(exp1g_wide) <- g.by.s_levels

exp_levels <- paste0("exp_", 1:4)
exp1g_wide[, experiment_id := rep(exp_levels, c(5,6,6,5))] #check!
exp1g_wide[, experiment_id := factor(experiment_id)] #check!

exp1g <- melt(exp1g_wide,
              id.vars = "experiment_id",
              measure.vars = g.by.s_levels,
              variable.name = "treatment",
              value.name = "gc") %>% # cell count
  na.omit()

exp1g[, c("genotype", "sex"):= tstrsplit(treatment,
                                             " ",
                                             fixed = TRUE)]
exp1g[, genotype := factor(genotype,
                           levels = genotype_levels)]
exp1g[, sex := factor(sex,
                           levels = sex_levels)]

exp1g_means <- exp1g[, .(gc = mean(gc)),
                     by = .(treatment, genotype, sex, experiment_id)]

intercept	slope 1	slope 2	slope 3
\(\gamma_{0.1}\)	\(\gamma_{1.1}\)	\(\gamma_{2.1}\)	\(\gamma_{3.1}\)
\(\gamma_{0.2}\)	\(\gamma_{1.2}\)	\(\gamma_{2.2}\)	\(\gamma_{3.2}\)
\(\gamma_{0.3}\)	\(\gamma_{1.3}\)	\(\gamma_{2.3}\)	\(\gamma_{3.3}\)
\(\gamma_{0.4}\)	\(\gamma_{1.4}\)	\(\gamma_{2.4}\)	\(\gamma_{3.4}\)

1	COR(\(\gamma_{0}\), \(\gamma_{1}\))	COR(\(\gamma_{0}\), \(\gamma_{2}\))	COR(\(\gamma_{0}\), \(\gamma_{3}\))
COR(\(\gamma_{1}\), \(\gamma_{0}\))	1	COR(\(\gamma_{1}\), \(\gamma_{2}\))	COR(\(\gamma_{1}\), \(\gamma_{3}\))
COR(\(\gamma_{2}\), \(\gamma_{0}\))	COR(\(\gamma_{2}\), \(\gamma_{1}\))	1	COR(\(\gamma_{2}\), \(\gamma_{3}\))
COR(\(\gamma_{3}\), \(\gamma_{0}\))	COR(\(\gamma_{3}\), \(\gamma_{1}\))	COR(\(\gamma_{3}\), \(\gamma_{2}\))	1

Chapter 16 Models for non-independence – linear mixed models

16.1 Liberal inference from pseudoreplication

16.2 Conservative inference from failure to identify blocks

16.3 Introduction to models for non-independent data (linear mixed models)

16.4 Experimental designs in experimental bench biology

16.4.1 Notation for models

16.4.2 Completely Randomized Design (CRD)

16.4.3 Completely Randomized Design with Subsampling (CRDS) or “Nested Design”

16.4.4 Randomized Complete Block Design (RCBD)

16.4.5 Randomized Split Plot Design (RSPD)

16.4.6 Generalized Randomized Complete Block Design (GRCBD)

16.4.7 Nested Randomized Complete Block Design (NRCBD)

16.4.8 Longitudinal Randomized Complete Block Design (LRCBD)

16.4.9 Variations due to multiple measures of the response variable

16.5 Building the linear (mixed) model for clustered data

16.6 Example 1 – A random intercepts and slopes explainer (demo1)

16.6.1 Batched measurements result in clustered residuals

16.6.2 Clustered residuals result in correlated error

16.6.3 In blocked designs, clustered residuals adds a variance component that masks treatment effects

16.6.4 Linear mixed models are linear models with added random factors

16.6.5 What the random effects are

16.6.6 In a blocked design, a linear model with added random effects increases precision of treatment effects

16.6.7 The correlation among random intercepts and slopes

16.6.8 Clustered residuals create heterogeneity among treatments

16.6.9 Linear mixed models are flexible

16.6.10 A random intercept only model

16.6.11 A model including an interaction intercept

16.6.12 AIC and model selection – which model to report?

16.6.13 The specification of random effects matters

16.6.14 Mixed Effect and Repeated Measures ANOVA

16.6.15 Pseudoreplication

16.7 Example 2 – experiments without subsampling replication (exp6g)

16.7.1 Understand the data

16.7.2 Model fit and inference

16.7.2.1 Fit the model

16.7.2.2 Inference from the model

16.7.2.3 Plot the model

16.7.2.4 Alternaplot the model

16.7.3 The model exp6g_m1 adds a random intercept but not a random slope

16.7.4 The fixed effect coefficients of model exp6g_m1

16.7.5 The random intercept coefficients of exp6g_m1

16.7.6 The random and residual variance and the intraclass correlation of model exp6g_m1

16.7.7 The linear mixed model exp6g_m1 increases precision of treatment effects, relative to a fixed effects model

16.7.8 Alternative models for exp6g

16.7.9 Paired t-tests and repeated measures ANOVA are special cases of linear mixed models

16.7.10 Classical (“univariate model”) repeated measures ANOVA of exp6g

16.7.11 “Multivariate model” repeated measures ANOVA

16.7.12 Linear mixed models vs repeated measures ANOVA

16.7.13 Modeling \(\texttt{mouse_id}\) as a fixed effect

16.8 Example 3 – Factorial experiments and no subsampling replicates (exp5c)

16.8.1 Understand the data

16.8.2 Examine the data

16.8.3 Model fit and inference

16.8.3.1 Check the model

16.8.3.2 Inference from the model

16.8.3.3 Plot the model

16.8.3.4 Alternaplot the model

16.8.4 Why we care about modeling batch in exp5c

16.8.5 The linear mixed model exp5c_m1 adds two random intercepts

16.8.6 The fixed effect coefficients of model exp5c_m1

16.8.7 The random effect coefficients of model exp5c_m1

16.8.8 Alternative models for exp5c

16.8.9 Classical (“univariate model”) repeated measures ANOVA

16.8.10 “Multivariate model” repeated measures ANOVA of exp5c

16.8.11 Modeling \(\texttt{donor}\) as a fixed effect

16.9 Example 4 – Experiments with subsampling replication (exp1g)

16.9.1 Understand the data

16.9.2 Examine the data

16.9.3 Fit the model

16.9.4 Inference from the model

16.9.5 Plot the model

16.9.6 Alternaplot the model

16.9.7 Understanding the alternative models

16.9.8 The VarCorr matrix of models exp1g_m1a and exp1g_m1b

16.9.9 The linear mixed model has more precision and power than the fixed effect model of batch means

16.9.10 Fixed effect models and pseudoreplication

16.9.11 Mixed-effect ANOVA

16.10 Statistical models for experimental designs

16.10.1 Models for Completely Randomized Designs (CRD)

16.10.2 Models for batched data (CRDS, RCBD, RSPD, GRCBD, NRCBD)