Chapter 18 Linear mixed models
18.1 Random effects
Researchers often collect data in batches, for example
- An ecologist interested in the effects of insectivorous birds on tree seedling performance in a forest stake out ten 1 m\(^2\) plots and use a wire-mesh cage to cover half of each plot.6 The cage allows insect herbivores into the seedlings inside but excludes insectivorous birds that eat the insects from the seedlings. In every plot, five seedlings are planted within the exclosure and five outside of the exclosure. At the end of the experiment, the total leaf mass is measured on each seedling. Small, uncontrolled, environmental factors (including soil factors and density of insectivorous birds) will differ between plots but will be common to all seedlings within a plot and we would expect a common response to this uncontrolled variation on top of the differential response to each treatment. As a consequence, the ten measures of leaf mass within a plot are not independent.
- A nutrition researcher wants to compare the effect of glucose vs. fructose on glucose metabolism in humans. Ten individuals are recruited. Each individual has blood insulin measured 60 minutes after a noon meal over six successive days. The meal alternates between high glucose and high fructose on each day. Each individual has three measures under high glucose treatment and three measures under high fructose treatment. Small, uncontrolled, environmental factors (including metabolic variation, other meals, activity levels) will differ between the individuals but be common within an individual and we would expect a common response to this uncontrolled variation on top of the differential response to each treatment. As a consequence, the six measures of insulin within an individual are not independent.
- An ecologist wants to measure the effect of an invasive plant on the reproduction of a native plant. They stake-out ten, 2 m\(^2\) plots in a forest and divide each plot into four quadrants, with each quadrant assigned a different treatment: control, activated carbon (a procedural control), extract from the invasive plant’s leaves, and both activated carbon and extract from the invasive plant’s leaves. The response is seedling count. Small, uncontrolled, environmental factors (including soil, drainage, and light) will differ between plots but will be common to all four quadrants within a plot and we would expect a common response to this uncontrolled variation on top of the differential response to each treatment. As a consequence, the four sets of counts within a plot are not independent.
- A physiologist has skeletal muscle cells growing in 5 control cultures, and 5 treated cultures. The \(Y\) variable is cell diameter, which is measured in 10 cells per culture. Small, uncontrolled, environmental factors (including chemical) will differ between cultures but will be common to all cells within a culture and we would expect a common response to this uncontrolled variation on top of the differential response to each treatment. As a consequence, the ten measures of diameter within a culture are not independent.
- A behavioral biologist wants to measure the effect of a predator fish on the preferred feeding location (open water or vegetation) of a prey fish. Ten tanks are set up with equal amounts of vegetated and unvegetated area. One-third of each tank is screened off to house a predator fish, which are added to five of the tanks. Ten prey fish are added to each tank. The response is minutes spent foraging in the open water as a fraction of total time foraging, which is measured in each fish in each tank. Small, uncontrolled, environmental factors (including temperature, water chemistry, light, and fish behavior) will differ between the tanks but be common within tanks and we would expect a common response to this uncontrolled variation on top of the differential response to each treatment. As a consequence, the ten measures of foraging of each fish within a tank are not independent.
- A microbiologist wants to measure the effect of the microbiome on autism-spectrum-disorder(ASD)-like behavior in mice7. Intestinal microbobial communities from five humans with ASD and five humans without ASD are transferred to germ-free mice via fecal transplant. Each human donor is used to colonize three mice. The response is time socializing in a direct social interaction. Uncontrolled features of each microbial community (species composition and proportions) will differ among human donors but will be the same within human donors and we would expect a common response to this uncontrolled variation in addition to any differential response to ASD-associated microbiota. As a consequence, the measures of behavior in the three mice within a donor group are not independent.
The batches – plots in experiment 1, individuals in experiment 2, plots in experiment 3, cultures in experiment 4, tanks in experiment 5, and mice in experiment 6 – are the experimental units, meaning that it is at this level that the experimenter is controlling the conditions. In each of these studies, there is systematic variation at two levels: among treatments due to treatment effects and among batches due to batch effects. This among-batch variation is the random effect. An assumption of modeling random effects is that the batches (plots/individuals/cultures/tanks/donor) are a random sample of the batches that could have been sampled. This is often not strictly true as batches are often convenience samples.
The multiple measures within a batch are subsamples but are often called repeated measures if the batch is an individual (experiment 2 is an example). If multiple measures within a treatment level within a batch (that is, within a \(batch \times treatment\) combination) are taken over time, the data are longitudinal. Not infrequently, subsamples within a treatment within a batch are called “replicates”, but this can be confusing because the treatments are replicated at the level of the batch and not at the level of the subsamples within a treatment by batch combination. The batches are the independent experimental units. The subsamples within a batch are not replicates.
The variation among batches/lack of independence within batches has different consequences on the uncertainty of the estimate of a treatment effect. The batches in experiments 1-3 are similar in that each contains all treatment levels. In these, the researcher is interested in the treatment effect but not the variation due to differences among the batches. The batches are nuissance factors that add additional variance to the response, with the consequence that estimates of treatment effects are less precise, unless the variance due to the batches is explicitly modeled. In experiments like 1-3, the batches are known as blocks. Including block structure in the design is known as blocking. Adding a blocking factor to a statistical mode is used to increase the precision of an estimated treatment effect.
Experiments 1 and 2 are examples of a randomized complete block with subsampling design. “Complete” means that each block has all treatment levels or combinations of levels if there is more than one factor. The subsampling is not replication. The replicates are the blocks, because it was at this level that treatment assignment was randomized. Experiment 3 is an example of a randomized complete block design. The blocks are complete but there is only one measure of the response per treatment.
The batches in experiments 4-6 are similar in that treatment is randomized to batch, so each batch contains only a single treatment level. In these segregated experimental designs, the variation among batches that arises from non-treatment related differences among batches confounds the variation among batches due to a true treatment effect. An extreme example of this would be experiment 4 (muscle cell cultures) with only a single culture with control conditions and a single culture with treatment conditions. Imagine 1) the true effect of the treatment is zero and 2) an unmeasured growth factor that happens to be more concentrated in the treatment culture at the beginning of the experiment. At the end of the experiment the cells in the treatment culture have an average diameter twice that of that in the control culture. The researcher is fooled into thinking that the treatment caused the increased growth. Again, the replicates are at the level of the cultures, because it was at this level that treatment assignment was randomized. This means the researcher has a single replicate (or, \(n=1\)) in each treatment level, regardless of the number of cells that are measured within each culture. A statistical analysis that uses the subsampling within a replicate as the sample size is an example of pseudoreplication (Hurlbert 1984 xxx).
18.2 Random effects in statistical models
In all of the above examples, the researcher is interested in the treatment effect but not the variation due to differences among the blocks. The blocks are nuissance factors that add additional variance to the response, with the consequence that estimates of treatment effects are less precise, unless the variance due to the blocks is explicitly modeled. Including block structure in the design and in the statistical model is known as blocking. A natural way to think about the block factor is as a random effect, meaning that plots in experiment 1 or the mice in experiment 3 are simply random samples from a population of plots or mice. Modeling this using the residual-error specification looks like
\[\begin{equation} y_{ij} = (\beta_{0} + \beta_{0j}) + (\beta_{1} + \beta_{1j}) x_i + \varepsilon_i \tag{18.1} \end{equation}\]
where \(i\) indexes the observation and \(j\) indexes the block (culture, plot, mouse, etc). The intercept parameter \(\beta_{0j}\) is a random intercept and the slope parameter \(\beta_{1j}\) is a random slope. The intercept for observation i (that is, its expected value when \(X=0\)) has a fixed component (\(\beta_0\)) that is common to all observations and a random component (\(\beta_{0j}\)) that is common within a block but differs among blocks (see table below). In the above equation, I’ve used parentheses to show how these combine into the random intercept that is unique for each block. Similarly, the random slope (treatment effect) has a fixed part (\(\beta_1\)) that is common to all observations and a random component (\(\beta_{1j}\)) that is common within a block but differs among blocks (see table below). Again, these are collected within a pair of parentheses in the equation above.
| block | \(b_0\) | \(b_{0j}\) | \(b_1\) | \(b_{1j}\) |
|---|---|---|---|---|
| 1 | \(b_0\) | \(b_{0,j=1}\) | \(b_1\) | \(b_{1,j=1}\) |
| 2 | \(b_0\) | \(b_{0,j=2}\) | \(b_1\) | \(b_{1,j=2}\) |
| 3 | \(b_0\) | \(b_{0,j=3}\) | \(b_1\) | \(b_{1,j=3}\) |
| 4 | \(b_0\) | \(b_{0,j=4}\) | \(b_1\) | \(b_{1,j=4}\) |
| 5 | \(b_0\) | \(b_{0,j=5}\) | \(b_1\) | \(b_{1,j=5}\) |
| 6 | \(b_0\) | \(b_{0,j=6}\) | \(b_1\) | \(b_{1,j=6}\) |
Linear mixed models are called “mixed models” because they are a mix of fixed and random factors. Another useful way to specify this model is to think about it hierarchically, using
\[\begin{align} y_{ij} &= \beta_{0j} + \beta_{1j}x_i + \varepsilon_i \\ \varepsilon_i &\sim N(0, \sigma) \\ \beta_{0j} &= \beta_{0} + N(0, \sigma_{0}) \\ \beta_{1j} &= \beta_{1} + N(0, \sigma_{1}) \tag{18.2} \end{align}\]
The first line states that the response is a function of a block-specific intercept and a block specific slope plus some error that is unique to each observation. The third and fourth lines state that these block-specific effects are themselves a function of a common effect and a random term that is unique to each block. That is, we have a hierarchical or multi-level structure to the model. Line 1 is the top level and the effects that are specified in line 1 are a function of effects at a second, lower level, which are specified in lines 3 and 4. Because of this structure, linear mixed models are sometimes called hierarchical or multi-level models.
Finally, it’s useful to think how to specify a linear mixed model using the random-draw specification, as this leads naturally to generalized linear mixed models, or GLMMs.
\[\begin{align} y_{ij} &\sim N(\mu_{ij}, \sigma) \\ \mu_{ij} &=\beta_{0j} + \beta_{1j}x_i \\ \beta_{0j} &\sim N(\beta_0, \sigma_0) \\ \beta_{1j} &\sim N(\beta_1, \sigma_1) \tag{18.3} \end{align}\]
18.3 Linear mixed models are flexible
The linear mixed model in Equation (18.1) specifies both a random intercept and a random slope but a researcher might limit the random effect to the intercept only, or less commonly, the slope only. Excluding the random slope from Equation (18.1) results in the model
\[\begin{equation} y_{ij} = (\beta_{0} + \beta_{0j}) + \beta_{1}x_i + \varepsilon_i \tag{18.4} \end{equation}\]
We might use a random-intercept-only model if we think that features of the block would effect the mean response among blocks but not effect the difference in treatment level (or treatment effect) among blocks. For example, differences in the immune systems among the individual mice in experiment 3 might effect growth in both the wild-type and engineered strains of staph but won’t effect the difference in growth between wild-type and engineered strains from one mouse to another.
Not more than you should know – For more complex mixed models, matrix algebra makes the specification of the model much more manageable than the scalar algebra in ??.
\[\begin{equation} \mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Zu} + \boldsymbol{\varepsilon} \end{equation}\]
where \(\mathbf{y}\) is the vector of the response, \(\mathbf{X}\boldsymbol{\beta}\) is the linear predictor of fixed effects and \(\mathbf{Zu}\) is the linear predictor of random effects. \(\mathbf{X}\) is the model matrix for the fixed effects and \(\boldsymbol{\beta}\) is the vector of fixed-effect terms (the fixed part of the intercept (\(\beta_0\)), including the fixed-effect coefficients for each of the
18.4 Blocking
18.4.1 Visualing variation due to blocks
To visualize random effects due to block, Let’s create fake data that look something like experiment 1, with a single factor with two treatment levels, \(k=10\) blocks, and \(n=3\) measures for each treatment level within each block. This is a randomized complete block design with subsampling and has a total of \(N=2 \times k \times n\) measures of \(Y\) (and rows of the data.table).
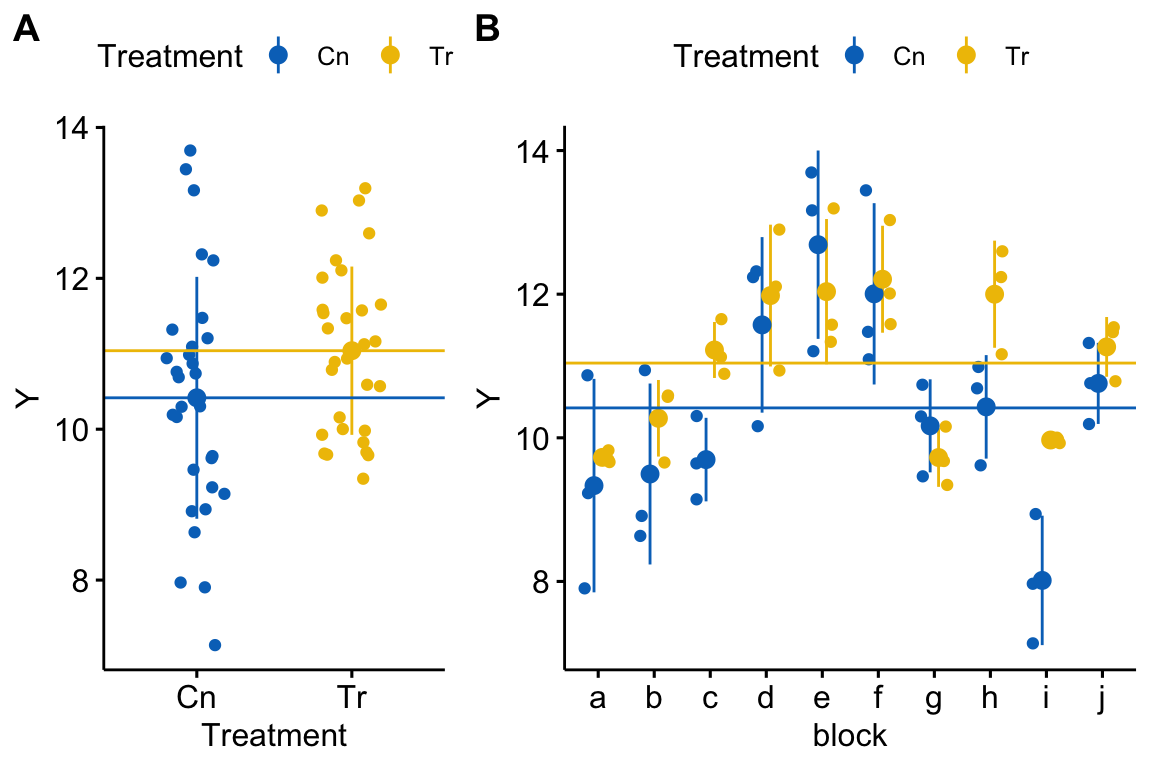
Figure 18.1: Visualizing random effects. A) The response in the two treatment levels. B) The same data but separated by block. The blue line is at the control mean and the yellow line is at the treated mean. The black dots are the mean response within a block.
Figure 18.1A shows the response as a function of treatment. The responses are nicely symmetric around the treatment means (the blue and yellow lines). A linear model (and generalized linear models, more generally) assumes that a response, conditional on the \(X\), are independent. Figure 18.1B shows how this assumption is violated for the simulated data. That pattern of residuals within a block around the treatment means does not look at all random. Instead, there is a distinct pattern within a block for the points to cluster either below the treatment means or above the treatment means. In blocks a, b, g, and i, all or most of the responses are below their treatment mean (for example in block b, all the yellow points are below the yellow line and two of three blue points are below the blue line). In blocks d, e, f, and j, all or most of the responses are above their treatment mean (for example, in block e, all three yellow points are above the yellow line and all three blue points are above the blue line). In other words, the responses within a block covary together. For a linear model, this is known as correlated error.
18.4.2 Blocking increases precision of point estimates
Block effects are differences in expected mean response among blocks due to unmeasured factors that are shared within blocks but not among blocks. A classical linear model fails to model this component of the total variance in the response, and as a consequence, this block-specific variance is part of the error variance. One way to think about this is by moving the random intercept and random slope components of equation (18.1) to the right and combining it with the observation-specific (or “conditional”) error (\(\varepsilon_i\))
\[\begin{equation} y_{ij} = \beta_{0} + \beta_{1} x_i + (\beta_{0j} + \beta_{1j} + \varepsilon_i) \tag{18.4} \end{equation}\]
A linear mixed model estimates the random effects parameters, so the residual from observation \(i\) is \(\varepsilon_i\). A linear model does not estimate the random effects parameters, so the residual of observation \(i\) from a linear model is \(\beta_{0j} + \beta_{1j} + \varepsilon_i\). Consequently, the error variance from a linear model is larger than the error variance from a linear mixed model fit to the same data. The consequence of this on inference depends on the variance of the random effects relative to the variance of the observation-specific error and on the subsample size. If the variance due to random effects is relatively big and subsample size is relatively small, then a linear mixed model estimates treatment effects with much more precision (and p-values will be smaller).
This increased precision is seen in the coefficient table of three models fit to the fake data in Figure 18.1.
A linear model fit to all data| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| TreatmentTr | 0.62441 | 0.3566 | 1.75 | 0.085 | -0.089 | 1.338 |
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| TreatmentTr | 0.62441 | 0.54713 | 1.14 | 0.269 | -0.525 | 1.774 |
| term | estimate | std.error | statistic | df | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|---|
| TreatmentTr | 0.62441 | 0.26995 | 2.31 | 9 | 0.046 | 0.095 | 1.154 |
Note that the estimates of treatment effect do not differ among models. What does differ is the estimated standard error of the treatment effect, which is 24% smaller in the linear mixed model relative to that in the linear model, and 51% smaller in the linear mixed model relative to that in the linear model fit to the block means. This difference in SE propogates to the confidence intervals and p-values.
Let’s explore this a wee bit more systematically using a simple, Monte Carlo simulation experiment. 5000 fake data sets were generated. Each data set simulated an experiment with a single treatment factor with two levels (“control” and “treatment”). The design is a randomized complete block with subsampling. There are 8 blocks and 3 subsamples in each treatment level per block. The treatment effect (\(\beta_1\)) is 1. The observation-specific (or “within-block”) variance (\(\sigma^2_{varepsilon}\)) is 1. The (“among-block”) variance of the random intercept (\(\sigma^2_{\beta_0j}\)) is 1 – the same as the the within-block variance. The variance variance of the random slope (\(\sigma^2_{\beta_1j}\)), which is due to a variable response of the treatment among blocks, is \(0.1^2\)).
The following three models were fit to all 5000 data sets
- a linear model fit to all data, ignoring blocks (violating the independence assumption)
- a linear model fit to the treatment means of the blocks (valid, but throwing out data)
- a linear mixed model that models the random intercept8.
From each fit, I saved the 95% confidence interval of the treatment effect and the p-value. The median width of the confidence interval and the power, which is the relative frequency of p-values less than 0.05. The simulation was re-run using the same parameters except setting the treatment effect (\(\beta_1\)) to 0. In this new simulation, the relative frequency of p-values less than 0.05 is the Type I error.
| Model | CI width | Power | Type I |
|---|---|---|---|
|
1.58 | 0.75 | 0.012 |
|
2.39 | 0.31 | 0.002 |
|
1.16 | 0.92 | 0.051 |
For data similar to that simulated, the linear mixed model using a blocking factor has much more power than the linear model ignoring block (and ignoring the lack of independence) or the linear model comparing the treatment level means of the blocks. This lost power in the two linear models is due to the conservative Type I error rate (extreme in the case of the linear model of the group means). One take-home lesson here is, don’t throw away perfectly good data if the design of the experiment includes a blocking factor!
18.5 Pseudoreplication
18.5.1 Visualizing pseduoreplication
Subsamples from batches are not replicates. Inference from a model fit to subsampled observations without modeling the batches is called pseudoreplication, a term famously coined by Hurlbert (1984). For data from a randomized complete block design, ignoring the batches in the model will typically result in larger standard errors, wider confidence intervals, and too conservative p-values. In a segregated experiment, with only a single treatment level per batch (like that in experiments 4-6 above), ignoring the lack of independence in the model has the opposite effect. Standard errors are too small. Confidence intervals are too narrow. P-values are too liberal. Type I error is inflated. Let’s visualize a pseudoreplicated data set like this.
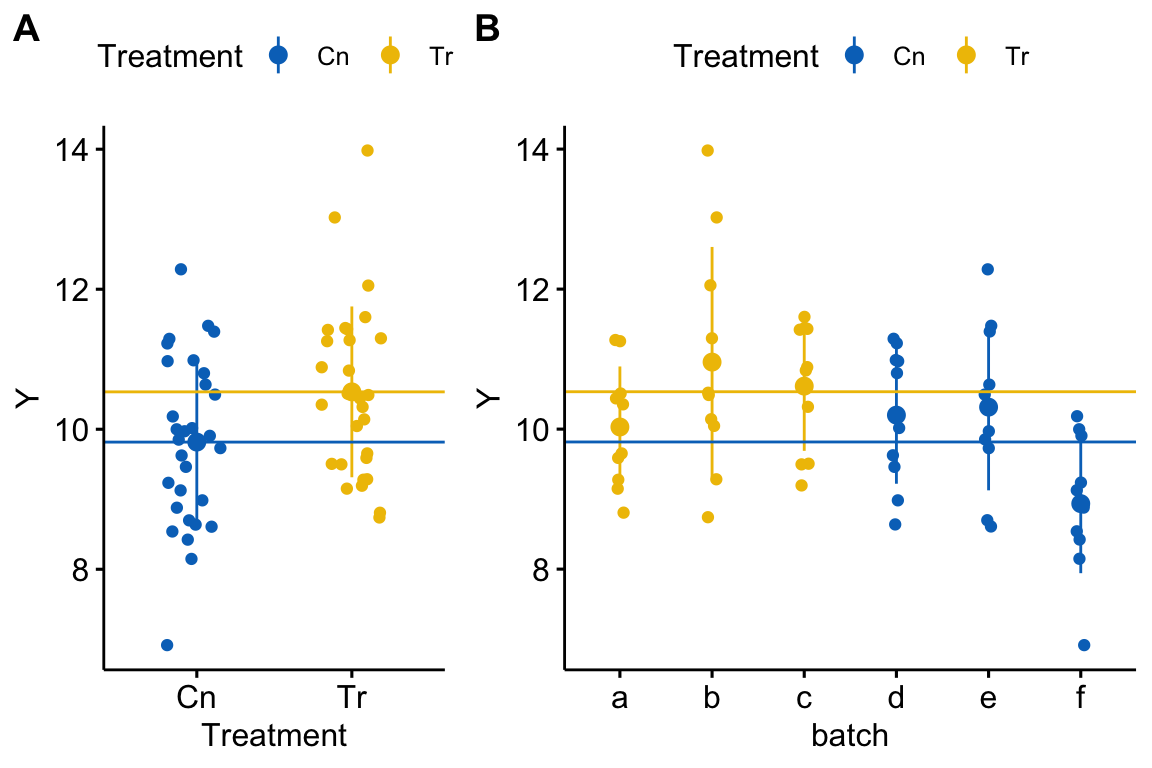
Figure 18.2: A data set in which treatment and batch are confounded because there is only one treatment level per batch.
This consequence of pseudoreplication when batch and treatment are confounded is seen in the coefficient table of four models fit to the fake data in Figure 18.2.
A linear model fit to all data (pseudoreplication).| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| TreatmentTr | 0.7175 | 0.31278 | 2.29 | 0.025 | 0.091 | 1.344 |
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| TreatmentTr | 0.7175 | 0.51803 | 1.39 | 0.238 | -0.721 | 2.156 |
| term | estimate | std.error | statistic | df | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|---|
| TreatmentTr | 0.7175 | 0.51797 | 1.39 | 3.32 | 0.252 | -0.298 | 1.733 |
| term | estimate | std.error | statistic | df | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|---|
| TreatmentTr | 0.7175 | 0.51803 | 1.39 | 4 | 0.238 | -0.298 | 1.733 |
As with the blocked design, all models compute the same estimate of the treatment effect. But in contrast to the blocked design, in this confounded design, the standard error of the treatment effect is smaller in the linear model of all data than that of the linear mixed models. This increased precision is an illusion because the model fails to account for the lack of independence within the batches.
One interesting result to note is the equivalence of the standard error, test statistic, p-value, and confidence intervals of the linear model on the batch means and the linear mixed model with a random intercept (but no random slope) only. The two are equivalent. Murtaugh (xxx) has argued that with this kind of design, it is much simpler to the analyst, and to your audience, to simply use the linear model on the batch means. This raises the question, why bother with subsampling within batch? One answer is, subsampling increases the precision of the batch mean, and therefore, the precision of the treatment effect. That said, the precision of a treatment effect is increased more efficiently by adding more replicates (more batches), not more subsamples.
Let’s explore the consequence of pseudoreplication with a confounded with a Monte Carlo simulation experiment. 5000 fake data sets were generated. Each data set simulated an experiment with a single treatment factor with two levels (“control” and “treatment”). The design is treatment level randomized to batch (only one treatment level per batch). There are 8 batches and 3 subsamples in each batch. The treatment effect (\(\beta_1\)) is zero. The observation-specific (or “within-block”) variance (\(\sigma^2_{varepsilon}\)) is 1. The (“among-block”) variance of the random intercept (\(\sigma^2_{\beta_0j}\)) is 1 – the same as the the within-block variance. The variance variance of the random slope (\(\sigma^2_{\beta_1j}\)), which is due to a variable response of the treatment among blocks, is \(0.1^2\)).
Because the effect is zero, the frequency of p-values less than 0.05 is the type I error. The same three models fit to the simulated blocked data are fit to these data. I don’t simulate an effect in order to compute power (at that effect size) because the increased power in the linear model of all data is, again, an illusion. It only comes at the cost of strongly elevated Type I error.
| Model | CI width | Type I |
|---|---|---|
|
2.22 | 0.18 |
|
3.80 | 0.05 |
|
3.80 | 0.05 |
When treatment level is randomized to batch, the type I error rate of a linear model fit to all data (and ignoring the lack of independence) is highly inflated. Don’t do this.
18.6 Mapping NHST to estimation: A paired t-test is a special case of a linear mixed model
Specifically, a paired t-test is equivalent to a linear mixed model with a single factor with two treatment levels, \(k\) blocks, and a single measure of each treatment level within each block. A good example is the wild type vs. engineered staph count in mice in experiment 3 above. A linear mixed model is much more flexible than a paired t-test because it allows a researcher to add treatment levels, additional factors, and covariates to the model. In addition, a linear mixed model can handle missing data.
Here is fake data similar in design to experiment 3 with a single factor with two treatment levels and both levels applied to the same experimental unit.
set.seed(2)
n <- 10 # number of mice (blocks)
x <- rep(c("WT","Tr"), each=n) # treatments
id <- rep(letters[1:n], 2) # block id
y <- c(rnorm(n, mean=10), rnorm(n, mean=11))
fake_data <- data.table(Y=y, X=x, ID=id)The t-test p-value is
## [1] 0.05336815and the coefficient table of the fixed effect in the linear mixed model is
## Value Std.Error DF t-value p-value
## (Intercept) 11.1797704 0.3438775 9 32.510914 1.212113e-10
## XWT -0.9686188 0.4358740 9 -2.222245 5.336815e-0218.7 Advanced topic – Linear mixed models shrink coefficients by partial pooling
In experiment 1 above, there are 10 sites (maybe different woodlots). In each plot, five seedlings are planted inside a cage and five outside the cage. The cage excludes insectivorous birds but not herbivorous insects. The researchers are investigating how birds affect plant growth indirectly – by eating insects that feed on the plants. The response is total leaf area in each seedling.
Let’s say we want to know the treatment effect in each of these sites. There are several ways of estimating this.
Fit \(k\) separate models, one for each site. The intercept (control mean) and slope (treatment effect) parameters for each site are estimated independently from all other sites. Consequently, the model parameters are computed using no pooling. For the estimation of the \(\beta\) terms, this is equivalent to a single, factorial linear model with \(Site\) modeled as a fixed effect (this is not true for the estimate of the standard errors of these terms since these are computed from the residual sum of squares of the model. For balanced data, all of the “intercept” or “slope” terms will have the same SE in the factorial analysis but differ among the \(k\) independent analyses).
Fit a linear model to all the data combined as if these were from a single site, and assign the intercept and treatment effect paramters to all sites. The model parameters are computed using complete pooling.
Fit a linear mixed model to all the data, using site as a random factor to estimate both random intercepts and slopes. Similar to the no-pooling analysis, there will be different intercept (control mean) and slope (treatment effect) estimates for each site, but unlike the no-pooling analysis, these estimates are computed by combining information from the other sites. The information used to estimate parameters in a linear mixed model is somewhere in between no pooling and complete pooling and is sometimes called partial pooling.
The consequence of partial pooling in a linear mixed model is that site intercepts (control means) are pulled toward the single intercept in the complete-pooling analysis and the site slopes (treatment effects) are pulled toward the single slope in the complete-pooling analysis. This has the consequence that the differences in parameter estimates among sites are shrunk toward zero. A consequence of this shrinkage is that the variance of the intercept estimates or of the slope estimates is smaller than that in the no-pooling analysis. Figure 18.3 shows this shrinkage effect using fake data simulating the seedling experiment.
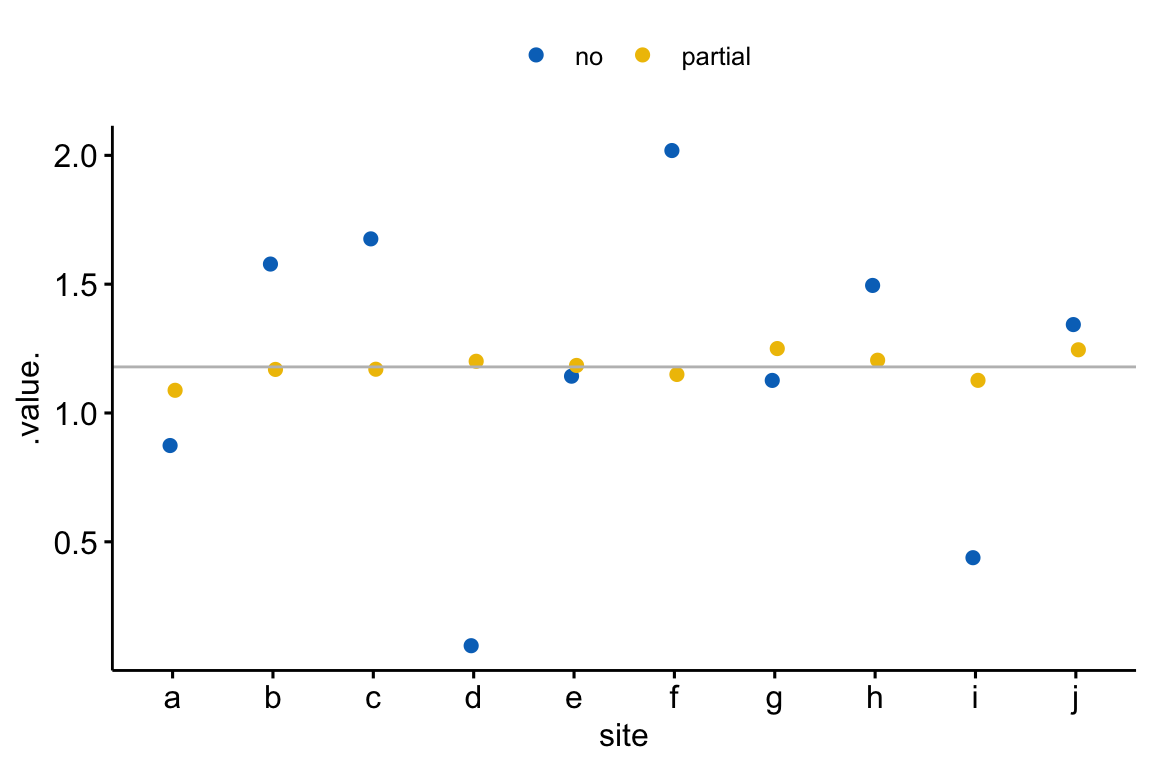
Figure 18.3: Shrinkage estimates of the treatment effect in a linear mixed model. The grey line is the estimate using complete pooling (so there is only one estimate which is assigned to each site). In general, the partial-pooling (linear mixed model) estimates (yellow) are generally closer to the complete pooling estimate than the no-pooling (separate linear models) estimates (blue). More specifically, if the no-pooling estimate is far from the complete pooling estimate, the partial pooling estimate is much closer to the complete pooling estimate. The consequence of partial pooling is that the differences among the estimates are shrunk toward zero.
The linear mixed model estimates of the treatment effects for each site are a type of shrinkage estimate and a linear mixed model is one kind of shrinkage estimator. Shrinkage estimates have fascinating properties:
- the variance of shrinkage estimates is less than that of ordinary least squares estimates (no-pooling, or using the block as a fixed factor)
- shrinkage estimates are biased but the OLS estimates are not. This means that the expected value of a coefficient from the linear mixed model does not equal the true (parameter) value! Or, more formally, \(\mathrm{E}(b_j) \ne \beta_j\).
- the mean square error of shrinkage estimates will be smaller than that for OLS estimates.
The first property was discussed above and shown in Figure 18.3. The second property raises the question, if we want to estimate the treatment effects within each site, why would we ever want to use \(Site\) as a random instead of fixed effect? The answer is the third property, which can be summarized as, “if we were to replicate the experiment many times, the shrinkage estimates will be, on average, less wrong (or closer to the true value) than the OLS estimates, where”wrong" is the absolute deviation from the true value."
When shrinkage estimators were first discovered, the third property surprised stasticians. The third property has profound consequences. Consider a scenario where researchers want to compare the performance of a new expression vector to that of an existing expression vector on protein production using E. coli. The researchers have ten different E. coli strains and are interested in strain-specific effects because they will choose the three strains with the largest effects for further testing. The researchers measure the response of each strain five times.
| Strain | \(\beta_{1j}\) | fixed \(b_{1j}\) | random \(b_{1j}\) |
|---|---|---|---|
| a | 0.91 | 1.07 | 0.98 |
| b | 0.87 | 0.94 | 0.85 |
| c | 0.90 | -1.03 | 0.30 |
| d | 0.81 | 0.64 | 0.63 |
| e | 1.09 | 1.00 | 1.07 |
| f | 0.62 | 0.91 | 1.14 |
| g | 1.33 | 2.26 | 1.36 |
| h | 1.27 | 1.48 | 0.96 |
| i | 1.61 | 0.57 | 1.13 |
| j | 0.89 | 1.50 | 0.93 |
The table above shows the true strain-specific effect and both the fixed (OLS) and random (LMM) effect estimates. The largest OLS estimate is 70% larger than the true effect and the strain with the largest true effect is not among the top three biggest OLS estimates (its ranking is 9/10). By contrast, the LMM estimates are closer to the true effects and the top strain is among the three largest LMM estimates.
These results are specific to these fake data but more generally, 1) the largest OLS estimates are inflated (larger error from the true effect), relative to the largest LMM estimates 2) overall, the LMM estimates will be closer than the OLS estimates to the true effects
To understand this, rank order the treatment effects for each strain. An individual strain’s position in this rank is the sum of the true effect for that strain and some random error. Because OLS, relative to shrinkage estimates, have greater variance in the estimate (that is, the random error component is bigger), the biggest effects estimated by OLS are more likely to be big because of the error component, compared to shrinkage estimates.
Not more than you want to know – Shrinkage estimators are not only useful when we are interested in block-specific effects but are also useful for estimating effects when there are multiple responses. For example, consider a researcher interested in measuring the effects of some exercise treatment on gene expression in adipose cells. The researcher measures expression levels in 10,000 genes. Given the typical content in undergraduate biostatics courses, a researcher would probably model these responses using 10,000 t-tests, or equivalently, 10,000 separate linear models. If the tests were ranked by \(p\)-value or absolute effect size, many of the genes with largest absolute effect would be there because of a large error component and many of the largest effects would be massively overinflated. Re-imagining the design as a single, linear mixed model with each gene modeled as a block would lead to a rank order in which the biggest measured effects more closely approximate the true effects.
18.8 Working in R
The major function for working with linear mixed models is lmer() from the lme4 package. An older, and still sometimes used and useful function is lme() from the nlme package. The authors of the lme4 package argue that the df in a linear mixed model are too approximate for a useful \(p\)-value and, consequently, the lme function does not return a \(p\)-value. Many biological researchers want a \(p\)-value and typically use the lmerTest package to get this.
Specifying a linear mixed model using lme. The random factor is in the column “block”. To conform to some packages that use lme4 objects, any variable used to model a random effect should be converted to type factor.
- add a random intercept using
y ~ treatment + (1|block). This adds a random intercept for each level of treatment. - add a random slope and intercept using
y ~ treatment + (treatment|block). This adds a random intercept for each level of treatment and a random slope for each level of treatment.
A message that might appear is “boundary (singular) fit: see ?isSingular”. This does not mean there is a problem with the fit model.
A warning that “Model failed to converge with 1 negative eigenvalue” does mean there is a problem. A solution is to simplify the model by, for example, removing a random slope.
18.8.1 coral data
Source Zill, J. A., Gil, M. A., & Osenberg, C. W. (2017). When environmental factors become stressors: interactive effects of vermetid gastropods and sedimentation on corals. Biology letters, 13(3), 20160957.
Dryad source https://datadryad.org/resource/doi:10.5061/dryad.p59n8
file name “VermetidSedimentData_ZillGilOsenberg_DRYAD.xlsx”
folder <- "Data from When environmental factors become stressors- interactive effects of vermetid gastropods and sedimentation on corals"
fn <- "VermetidSedimentData_ZillGilOsenberg_DRYAD.xlsx"
sheet_i <- "Coral Growth Rate Data"
file_path <- here(data_path, folder, fn)
coral <- read_excel(file_path, sheet=sheet_i) %>%
clean_names() %>%
data.table()
coral[, vermetids:=factor(vermetids)]
coral[, sediment:=factor(sediment)]
# recode levels of factors since 0 and 1
coral[, vermetids := fct_recode(vermetids,
absent = "0",
present = "1")]
coral[, sediment := fct_recode(sediment,
control = "0",
addition = "1")]18.8.1.1 Fitting models
# to reproduce the results
# observation 2 should be excluded from the analysis
inc <- c(1, 3:nrow(coral))
# random intercept only
m1 <- lmer(growth_rate ~ vermetids*sediment + (1|block), data=coral[inc])
# random intercept and slope
m2 <- lmer(growth_rate ~ vermetids*sediment + (vermetids|block) + (sediment|block), data=coral[inc])
# to include the interaction as a random effect we'd need subsampling within each factorial treatment combinationThe conditional effects of m1 are
# results using lmer fit
fit.emm <- emmeans(m1, specs=c("vermetids", "sediment"))
summary(contrast(fit.emm,
method = "revpairwise",
simple = "each",
combine = TRUE,
adjust="none"),
infer=c(TRUE, TRUE))## sediment vermetids contrast estimate SE df lower.CL
## control . present - absent 0.00466 0.209 23.0 -0.428
## addition . present - absent -0.76889 0.217 23.6 -1.217
## . absent addition - control 0.28520 0.217 23.6 -0.163
## . present addition - control -0.48834 0.209 23.0 -0.921
## upper.CL t.ratio p.value
## 0.4373 0.022 0.9824
## -0.3211 -3.547 0.0017
## 0.7330 1.316 0.2009
## -0.0557 -2.335 0.0286
##
## Degrees-of-freedom method: kenward-roger
## Confidence level used: 0.95There is no “correct” way to compute the degrees of freedom for inferential statistics (SE, CIs, p-values). Two common choices are “Kenward-Roger” and “Satterthwaite”. There is little empirical reason to vastly prefer one over the other (they each seem to perform a wee bit bitter under different conditions).
In emmeans, the Kenward-Roger degrees of freedom are the default. For Satterthwaite, use the lmer.df argument:
fit.emm <- emmeans(m1,
specs=c("vermetids", "sediment"),
lmer.df = "satterthwaite")
summary(contrast(fit.emm,
method = "revpairwise",
simple = "each",
combine = TRUE,
adjust="none"),
infer=c(TRUE, TRUE))## sediment vermetids contrast estimate SE df lower.CL
## control . present - absent 0.00466 0.209 22.9 -0.428
## addition . present - absent -0.76889 0.216 23.5 -1.215
## . absent addition - control 0.28520 0.216 23.5 -0.161
## . present addition - control -0.48834 0.209 22.9 -0.921
## upper.CL t.ratio p.value
## 0.4374 0.022 0.9824
## -0.3226 -3.559 0.0016
## 0.7315 1.320 0.1994
## -0.0556 -2.335 0.0287
##
## Degrees-of-freedom method: satterthwaite
## Confidence level used: 0.95If you want to compute the coefficient table or an ANOVA, lmer does not output test statistics. To get test statistics, you have to load the library “lmerTest” (which automatically loads “lme4”). With lmerTest, the Satterthwaite degrees of freedom are the default. For Kenward-Roger, use the ddf argument in either summary() (for the coefficients) or anova() (for ANOVA).
## Estimate Std. Error df
## (Intercept) 1.268411111 0.1541680 30.42768
## vermetidspresent 0.004655556 0.2091398 22.94243
## sedimentaddition 0.285202305 0.2160126 23.53130
## vermetidspresent:sedimentaddition -0.773546750 0.3006674 23.24638
## t value Pr(>|t|)
## (Intercept) 8.22745788 3.129900e-09
## vermetidspresent 0.02226049 9.824326e-01
## sedimentaddition 1.32030428 1.994327e-01
## vermetidspresent:sedimentaddition -2.57276556 1.693404e-02## Estimate Std. Error df
## (Intercept) 1.268411111 0.1541680 30.43671
## vermetidspresent 0.004655556 0.2091398 23.03604
## sedimentaddition 0.285202305 0.2167687 23.62024
## vermetidspresent:sedimentaddition -0.773546750 0.3012111 23.33762
## t value Pr(>|t|)
## (Intercept) 8.22745788 3.122797e-09
## vermetidspresent 0.02226049 9.824319e-01
## sedimentaddition 1.31569876 2.009032e-01
## vermetidspresent:sedimentaddition -2.56812158 1.708128e-02Compare the output from emmeans and coef(summary()) using the different methods for computing the df.