Chapter 16 ANOVA Tables

Treatment effects are most often analyzed using ANOVA, which is short for “Analysis of Variance”. This is somewhat of an odd name for a method to test for treatments effects - what do differences in means have to do with an analyis of variance? The name makes sense in light of the decomposition of the total variance into a model variance and the residual variance (chapter xxx). If there are differences among the means, then the total variance is increased because of variation among groups.

The engine underneath modern ANOVA is a linear model. If the model has a single categorical factor, the ANOVA is one-way. If the model has two categorical factors it is a two-way ANOVA. If the model has a single categorical factor and one continuous factor it is an ANCOVA, short for analysis of covariance (next chapter). More complex experimental designs classically analyzed with ANOVA are nested, split-plot, latin-square, and many others.

16.1 Summary of usage

If you choose to report an ANOVA, also report the effects and their uncertainty in some way, either the model coefficients or contrasts.

  1. ANOVA generates a table with one row for each term in the linear model. A term is a factor or a covariate or an interaction. For a two-way factorial ANOVA, these terms are the two main effects and the interaction effect.
  2. The ANOVA generates an \(F\) and \(p\)-value for the whole model and for each term in the ANOVA table.
  3. The \(p\)-value of an interaction term is often used as a decision rule to interpret the main effects. If \(p \le 0.05\) then do not interpret the main effects but instead examine the condition (“simple”) effects. If \(p > 0.05\), then interpret the main effects. Regardless, this sort of decision rule is itself controversial, and for good reason.
  4. If the main effects are to be interpreted, some statisticians advocate re-fitting the model without the interaction effect, others advocate interpreting the main effects with the interaction term in the model. This only matters if the design is unbalanced (see below).
  5. Regardles of any decision, always plot the data using a Harrell plot or interaction plot to understand and communicate the magnitude and pattern of interaction.
  6. For factors with more than two levels, the \(p\)-value is often used as a decision rule to dissect the factor with post-hoc tests, such as Tukey HSD.
  7. A design is balanced if all the cells have the same number of replicates. A design is unbalanced if one or more of the cells has a different number of replicates. Unbalanced designs make it necessary to make decisions, none of which are perfect, and all of which are controversial. Some statisticians have even advocated randomly excluding data until the design is back in balance. Don’t do this.
  8. There are multiple ways to decompose the sum of squares. I highlight the major three: Type I (sequential), Type II (partial sequential), and Type III. Most statistics software and introductory statistics books default to Type III and, consequently, many researchers are unaware that Types I and II exist. R’s default is Type I, and this can make a difference if the design is unbalanced. This is not a rare error in publications.
  9. Because R defaults to Type I sum of squares, the \(p\)-value of a factor depends on the order of the factors in the model if the design is unbalanced. This is a feature, not a bug.
  10. ANOVA based on type II sum of squares do not depend on factor order if the design is unbalanced, but it does assume that the interaction is zero.
  11. ANOVA based on type III sum of squares do not depend on order if the design is unbalanced and does not assume the interaction is zero.
  12. If the design is balanced, Type I, II, and III sum of squares generate the same ANOVA table. And the ANOVA table of just the main effects is the same as the ANOVA table that includes the interaction term. None of this is true when the design is unbalanced, However, the decision to use type II or type III is very controversial.

16.2 Example: a one-way ANOVA using the vole data

The vole data has a single factor (“treatment”) with three levels (“control”, “vitamin_E”, “vitamin_C”). In statistics textbooks that emphasize hypothesis testing, the “Which test should I use” flowchart would guide a researcher given this design to a single classification, or one-way ANOVA, since a t-test can only compare two levels but an ANOVA can compare more than two levels. There are better ways to think about what ANOVA is doing, but okay.

Here is an ANOVA table of the vole data:

Df Sum Sq Mean Sq F value Pr(>F)
treatment 2 248446 124223.0 2.95 0.057
Residuals 93 3912751 42072.6

I’ll explain all the parts of the ANOVA table later, but for now, focus on the \(p\)-value, which is that most researchers want out of the table. What null hypothesis does this \(p\)-value test? The p-value gives the probability of the observed \(F\) or larger \(F\), if the null were true. The null hypothesis models the data as if they were sampled from a single, normal distribution and randomly assigned to different groups. Thus the null hypotheis includes the equality of the means among factor levels. In the vole data, the single treatment factor has three levels and a small \(p\)-value could occur because of a difference in means between the vitamin_E treatment and control, or between the vitamin_C treatment and control, or between the two vitamin treatments. The \(p\)-value or ANOVA table doesn’t indicate what is different, only that the observed \(F\) is unexpectedly large if the null were true. As a consequence, researchers typically interpret a low \(p\)-value in an ANOVA table as evidence of “an effect” of the term but have to use additional tools to dissect this effect. The typical additional tools are either planned comparisons, which are contrasts among a subset of a priori identified treatment levels (or groups of levels) or unplanned comparisons (“post-hoc” tests) among all pairs of levels.

The \(p\)-value in the ANOVA table acts as a decision rule: if \(p < 0.05\) then it is okay to further dissect the factor with planned comparisons or post-hoc tests because the significant \(p\) “protects” the type I error of further comparisons. I’m not fond of using \(p\)-values for these sorts of decision rules.

16.3 Example: a two-way ANOVA using the urchin data

Let’s use the urchin data from the previous chapter xxx to explore the ANOVA table, which is what is typically reported. The experiment has two factors (\(Temp\) and \(CO2\)), each with two levels. Here is the linear model

\[\begin{equation} Resp = \beta_0 + \beta_1 Temp + \beta_2 CO2 + \beta_3 TempCO2 + \varepsilon \end{equation}\]

In order to understand factorial ANOVA (or any ANOVA with multiple factors), it is useful to know the difference between conditional means and marginal means

##          CO2-  CO2+ Temp-mm
## Temp-   8.233 7.917   8.075
## Temp+  12.743 9.742  11.243
## CO2-mm 10.488 8.829   9.659

In the table above, the upper, left \(2 \times 2\) grid of cells are the conditional means, which are the means of each group, where a group is a specific combination of factor levels. The first two values of the third row are the marginal means for CO2. The first (10.488) is the mean of the two means when CO2=CO2-. This can be written as \(\mathrm{E}(Resp|CO2-)\). The second (8.829) is the mean of the two means when CO2=CO2+, or \(\mathrm{E}(Resp|CO2+)\). The first two elements of the third column are the marginal means for Temp. These are \(\mathrm{E}(Resp|Temp-)\) and \(\mathrm{E}(Resp|Temp+)\). The bottom right value (9.659) is the grand mean.

A conditional effect is a difference between conditional means. For example the conditional effect of \(Temp\) conditional on CO2=CO2- is \(12.743-8.233\). A marginal effect is a difference in marginal means within a factor, for example the marginal effect of \(Temp\) is \(11.243 - 8.075\).

Here is the ANOVA table of the urchin data

Df Sum Sq Mean Sq F value Pr(>F)
Temp 1 60.2 60.2 19.1 0.0003
CO2 1 16.5 16.5 5.2 0.0332
Temp:CO2 1 10.8 10.8 3.4 0.0791
Residuals 20 63.2 3.2

This ANOVA table uses what are called Type 3 sum of squares, which is NOT the default in R but is the default in many other statistics software and is, therefore, the only type of ANOVA that many researchers know (and, many researchers are unaware that there are multiple types of ANOVA table). Understanding these differences is important, at least if one is reporting ANOVA tables. I’ll return to the importance of this later.

16.3.1 How to read an ANOVA table

An ANOVA table has a row for each term in the underlying linear model – each of these adds a component of variance to the total, and a row for the residual variance (this residual variance row is frequently excluded from the published table). The urchin model has three terms (one level of \(Temp\), one level of \(CO2\), and one interaction). The statistics for each term are

  1. Degrees of Freedom (df) – If the term is a factor, the df will equal the number of levels (\(k\)) for the factor minus 1. Think of it this way: the contribution of the variance due to a factor is a function of the variability of the \(k\) level means around the grand mean. How many degrees of independent variation do these level means have, given that we know the grand mean? The answer is \(k-1\) – once the values of \(k-1\) level means are written down, the \(k\)th level mean has no freedom to vary; its value has to be \(k\bar{\bar{Y}} - \sum_i^{k-1}{Y_i}\). For an interaction term, the df is the product of the df of each of the factors in the interaction.
  2. Sum of Squares – the sum of squared differences between the modeled value and the grand mean. In addition to a sum of squares for each term, a residual mean square is computed as the sum of squared differences between the measured and modeled values.
  3. Mean Square – The sum of squares divided by the df (this is a “mean” with df acting as the number of things that were summed).
  4. F-ratio – the Mean Square of the term dived by the residual mean square.
  5. p-value – the p-value for the F-ratio. F is compared to an F-distribution, which is a distribution of F-ratios under the null.

16.3.1.1 Each row in the table tests a null hypothesis

The row for each term in an ANOVA table tests a null hypothesis. In order to understand the null hypotheses, I need to define a few more terms

For the ANOVA table above, which uses Type 3 sum of squares, the probabilities are

  1. Temp – \(p = \mathrm{prob}(F \ge F_o|CO2, Temp:CO2)\). The null is no difference in means conditional on the level of CO2 and Temp:CO2. This is equivalent to no difference between the grand mean and the marginal mean of Temp+, or

\[\begin{equation} b_1 = \overline{\overline{Resp}} - \mathrm{E}(Resp|Temp^+) \end{equation}\]

  1. CO2– \(p = \mathrm{prob}(F \ge F_o|Temp, Temp:CO2)\). The null is no difference in means conditional on the level of Temp and Temp:CO2. This is equivalent to no difference between the grand mean and the marginal mean of CO2+, or

\[\begin{equation} b_2 = \overline{\overline{Resp}} - \mathrm{E}(Resp|CO2^+) \end{equation}\]

  1. Temp:CO2 – \(p = \mathrm{prob}(F \ge F_o|Temp, CO2)\). The null is no difference in means conditional on the level of Temp and CO2. This is equivalent to the difference between the conditional mean of Temp+/CO2+ and the expected conditional mean of Temp+/CO2+ if there were no interaction.

\[\begin{equation} b_3 = \mathrm{E}(Resp|Temp^+, CO2^+) - (\overline{\overline{Resp}} - b_1 - b_2) \end{equation}\]

As noted in the equations, these three differences are the coefficients of the linear model behind the ANOVA. Here is the coefficient table

Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.66 0.36 26.6 0.00000
Temp1 -1.58 0.36 -4.4 0.00030
CO21 0.83 0.36 2.3 0.03325
Temp1:CO21 -0.67 0.36 -1.9 0.07910

In ANOVA with type 3 sum of squares, the dummy variables are coded using effect coding, which differs from the dummy coding introduced in chapter xxx. The consequence is that the grand mean (the mean of \(Resp\) across all values) is now the “reference” value. The intercept in this table, then, is the grand mean. The coefficients are differences from the grand mean, as described above.

Use the table of conditional and marginal effects above to check that the coefficients equal the differences in the equations above. Also not that the \(p\)-values for the effects in the coefficient table equals the \(p\)-values in the ANOVA table.

It is important to note that this table differs from the coefficient table with dummy coding because that reference is the mean of Temp-/CO2- and not the grand mean.

Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.23 0.73 11.3 0.00000
TempTemp+ 4.51 1.03 4.4 0.00028
CO2CO2+ -0.32 1.03 -0.3 0.76081
TempTemp+:CO2CO2+ -2.68 1.45 -1.9 0.07910

Importantly, note that \(p\)-values for \(b_1\) (the Temp effect) and \(b_2\) differ between the two tables. This is because the \(t\)-value tests different hypotheses! In the coefficient table with effect coding (that behind the ANOVA with type 3 sums of squares), the \(p\)-value tests marginal effects and so is a function of both marginal means within a factor. By contrast, in the coefficient table with dummy coding, the \(p\)-value tests conditional effects, and so is only a function of the conditional means when the other factor is at its reference level (right? The coefficient \(b_1\) in the dummy coded coefficient table is the effect of only increasing \(Temp\) – \(CO2\) is left at its reference level). For the interaction effect, the coefficient differs between the effects coded model and the dummy coded model (because different reference means) but the \(p\)-value ultimately tests the same hypothesis (non-additive effects of the factors) and so the \(t\) and \(p\) values are the same.

16.3.1.2 What to do after ANOVA?

Researchers frequently report ANOVA statistics (\(F\) and \(p\) values) for factorial models in a way that suggests that they misunderstand the hypotheses tested. It probably doesn’t help that there is a long-standing debate among statisticians about the most sensible strategy for interpreting factorial ANOVA results. And it doesn’t help that the default ANOVA table in R can suggest a very different interpretation than the default ANOVA table in some other software packages.

Here are three strategies for interpreting a factorial ANOVA table that uses Type III sum of squares. All strategies use \(p\)-values to make a series of decision rules. In the first strategy, which is a type of model simplification or model selection, a researcher starts with the interactions at the bottom of the ANOVA table and works up, eliminating terms with \(p > 0.05\) and re-fitting the reduced model before interpreting main effects. In the second strategy, the researcher uses the original ANOVA table that includes all terms to interpret main effects.

Strategy 1

  1. is interaction p < 0.05?
    1. if yes, then do NOT test main effects. Show a graph to show pattern of conditional effects. Test conditional effects if this is of interest.
    2. if no, then refit model without the interaction and test main effects – This now is equivalent to ANOVA using Type II sum of squares.
      1. is main effect p < 0.05$?
        1. if yes, then keep in model
        2. if no, then refit model without that main effect

Strategy 2

  1. is interaction p < 0.05?
    1. if yes, then do NOT test main effects. Show a graph to show pattern of conditional effects. Test conditional effects if this is of interest.
    2. if no, then use the same table as the test of the main effects. This is interpreting the main effects with the interaction term in the model. This is the logic of ANOVA using type III sum of squares.

Strategy 3

  1. is interaction p < 0.05?
    1. if yes, then look at interaction plot to determine if it makes sense test main effects. For example, if CO2+ had obviously lower \(Resp\) at both levels of \(Temp\), even if one was much lower (ie. interactaction), then some people would say that the test of the main effect is meaningful. Test conditional effects if this is of interest.
    2. if no, then use the same table as the test of the main effects

In general, statisticians advise against strategy 3 (interpreting main effects in the presence of interaction) – its not wrong, its just that a main effect has an awkward interpretation if there is an interaction. Of course this is true if there is any interaction term in the model, not just a statistically significant term. The controversy is more, if the interaction \(p\) is not significant, then do we implement stategy 1 (refit model excluding interaction to test main effects) or strategy 2 (use full factorial anova table to test main effects).

Df Sum Sq Mean Sq F value Pr(>F)
Temp 1 45.2 45.2 14.5 0.0011
CO2 1 4.1 4.1 1.3 0.2630
Temp:CO2 1 14.8 14.8 4.8 0.0413

then one shouldn’t report the ANOVA results using something like “Temperature had a significant effect on metabolism (\(F_{1,20} = 14.5\), \(p=0.001\)). There was no effect of CO2 on metabolism (\(F_{1,20} = 4.1\), \(p=0.26\))”. There was a significant interaction effect between Temperature and CO2 on metabolism (\(F_{1,20} = 14.8\), \(p=0.04\))". If one accepts that the small interaction \(p\)-value is evidence of an interaction effect then this interpretation of the main factors makes no sense, as the first two results imply that the interaction effect is zero (or, that there is a constant effect of \(Temp\) or \(CO2\) across both levels of the other factor), which is then contradicted by the third result.

More specifically, if one is using a \(p\)-value to guide decision making, then a significant interaction \(p\) indicates that there is no single “main” effect of a factor. Instead, the effect of \(Temp\) is conditional on the level of \(CO2\), and the effect of \(CO2\) is conditional on the level of \(Temp\). This is easily seen in the interaction plot, where the effect of \(Temp\) is large when \(CO2\) is high but much smaller when \(CO2\) is low. Indeed, the effect of \(Temp\) at the low CO2 is 0.16.

Instead of interpreting the factors as constant effects, A better strategy is to compare the conditional effects, that is, the effects of \(Temp\) within each level of \(CO2\) and the effects of \(CO2\) within each level of \(Temp\) (conditional effects are sometimes called the “simple effects”).

The controversy arises in what to do after an ANOVA if the interaction effect has a non-significant \(p\)-value. At this point, I am punting instead of explaining the basis for the controversy, because ultimately I think the major problem with both strategies is the use of null hypothesis significance testing to make analysis decisions.

In fact, the entire reason that I use the urchin data as the example for factorial ANOVA is because it beautifully illustrates the absurdity of the interaction \(p\)-value decision rule. Why should we interpret the results of the ANOVA when the interaction \(p\) is 0.079 differently than when the interaction \(p\) is 0.04? Remember, the \(p\)-value is a “sample” statistic (in the sense that it is entirely a function of the sampled data) and in conditions of low power (which is likely, but not necessarily, true for the urchin data given n=6), a \(p\)-value is highly variable.

There are several problems with this approach. 1) a \(p\)-value is not evidence of “no effect”, 2) the power to test interaction effects is small relative to that for the main effects (this is a general rule, not something specific to these data), 3) the interaction SS accounts for about 7.2\(\%\) of the total SS, which doesn’t seem inconsequential, and 4) the interaction \(p\)-value is small enough to raise a red flag, and, most importantly, 5) the confidence interval of the interaction effect indicates that the large, negative values of the interaction are as consistent with the data as trivially small values (or a value of zero). But the CI is not in an ANOVA table and many researchers fail to report it. These five points suggest that this experiment be replicated, with a larger sample size, to get a better estimate of the interaction effect. The problem of course is that experiments are rarely replicated, except in biomedical research.

The absurdity of the \(p\)-value decision rule strategy for interpretation of effects after an ANOVA is highlighted by comparing the forest plot of model coefficients of the real and fake urchin data. It would be absurd to use an ANOVA table to interpret these patterns as radically different (one without an interaction and constant main effects, the other with an interactioni and conditional effects).

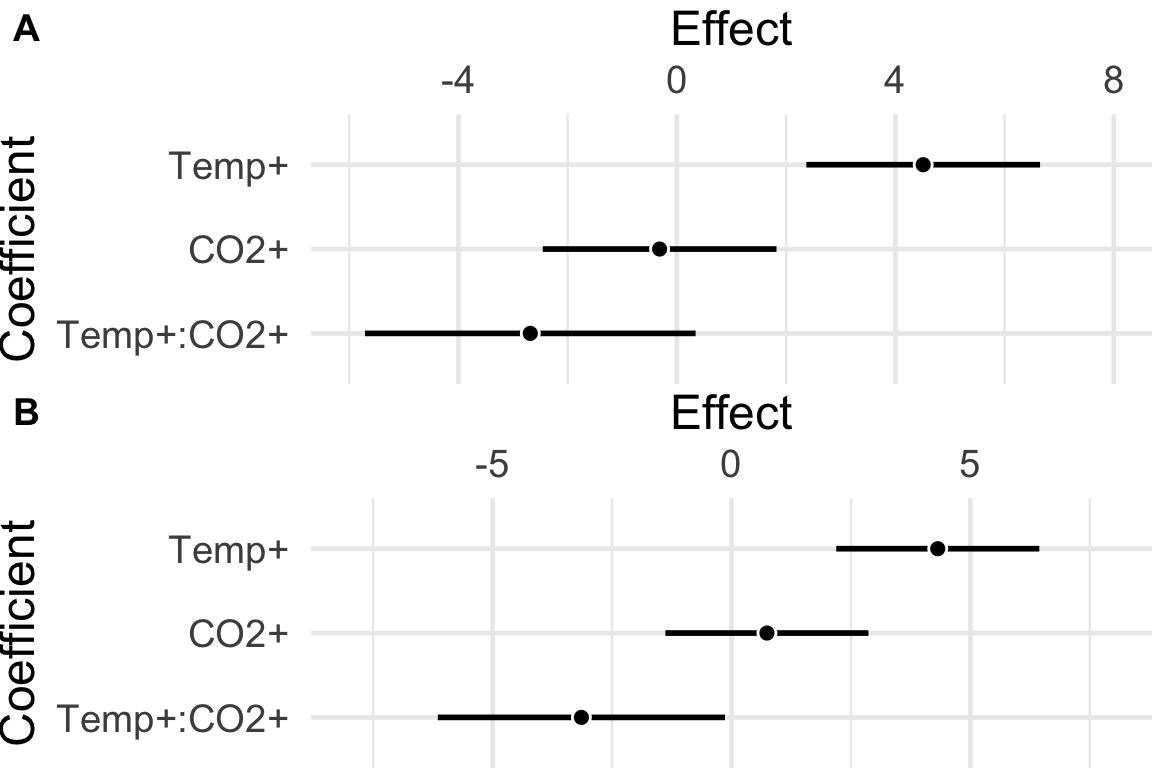
Forest plots (the upper part of a Harrell plot) of the actual and fake urchin data. A) Real urchin data. The interaction effect is not significant ($p=0.079$). B) Fake urchin data. The interaction effect is significant ($p=0.04$).

Figure 16.1: Forest plots (the upper part of a Harrell plot) of the actual and fake urchin data. A) Real urchin data. The interaction effect is not significant (\(p=0.079\)). B) Fake urchin data. The interaction effect is significant (\(p=0.04\)).

16.3.2 How to read ANOVA results reported in the text

ANOVA results are often reported in the text of a results section, using something like “Temperature had a significant effect on metabolism (\(F_{1,20} = 14.5\), \(p=0.001\)). There was no effect of CO2 on metabolism (\(F_{1,20} = 4.1\), \(p=0.26\))”. The subscripts of the \(F\) statistic are the numerator and denominator degrees of freedom (df) of the \(F\)-value (These df are a column in the ANOVA table. The denomintor df may not appear in the table if it is the residual df and the row for the residual term was not reported). Sometimes I find the reported df are not consistent with the description of the design and analysis, which means the data were not analyzed as stated.

16.3.3 Better practice – estimates and their uncertainty

As emphasized in the previous chapter, the decision to include or exclude an interaction effect in the model should not be based on a \(p\)-value but on the goals of the model.

  1. If the goal is the interaction (because a scientific model predicts one, or because this is biology and everything is conditional), then estimate the interaction effect (as a coefficient of the model!) and its uncertainty, including a CI and \(p\)-value. There is no controversy on how to estimate this effect and its uncertainty. The coefficient will be different between dummy and effect coded models but this is okay because they have different specific interpretations but the same general interpretation. Use a Harrel plot with the coefficients (including the interaction coefficient) to show this estimate and uncertainty.

  2. If the goal is to estimate constant main effects, then exclude the interaction effect from the model and report the main effects (again, as coefficients from the model or contrasts if other pairwise effects are desired) with their uncertainty. Use an interaction plot (or bottom part of the harrell plot) to justify forcing the interaction to zero (for example the interaction effect adds little to the total sum of squares or the interpretation of a single main effect or two (or more) conditional effects would be the same. Use a Harrel plot that excludes the interaction term to show these main effects and uncertainty.

  3. And if a researcher is interested in the effects of the factors but there is strong evidence for a non-trivial interaction, then report the conditional effects (as contrasts) with their uncertainty. Use a Harrel plot that includes the interaction term to show these conditional effects and uncertainty. If there is an obvious interaction, it probably doesn’t make sense to interpret the main effects, contrary to what some people argue. If there is a positive effect of factor A across all levels of factor B, we don’t really need a \(p\)-value to test that the average of these positive effects is significant. This doesn’t add value to the plot and any conditional effects that are reported.

Notice that an ANOVA table has no role in this recommendation.

16.4 Unbalanced designs

My recommendation above is to not bother with ANOVA, but to simply compute the contrasts of interest using the linear model. But if you really want to use ANOVA, you should be aware that if the design is unbalanced, factor order matters in the default R anova function and that I routinely find published ANOVA tables that report statistics (\(F\) and \(p\) values) that are not what the authors think they are.

An unbalanced design is one in which the number of replicates differs among the cell. The urchin data is balanced because there are six replicates in each cell. If the respirometer broke before taking the respiratory measures of the final tank, the design would be unbalanced, one of the cells would have only five replicates.

Let’s look at the effect of row order on the statistics of the urchin data using R’s default anova function.

Df Sum Sq Mean Sq F value Pr(>F)
Temp 1 60.20 60.20 19.06 0.00030
CO2 1 16.52 16.52 5.23 0.03325
Temp:CO2 1 10.81 10.81 3.42 0.07910
Df Sum Sq Mean Sq F value Pr(>F)
CO2 1 16.52 16.52 5.23 0.03325
Temp 1 60.20 60.20 19.06 0.00030
CO2:Temp 1 10.81 10.81 3.42 0.07910

Now let’s unbalance the data, by removing three random replicates (these may be both in one cell or spread across cells. First, here is the number of replicates in each cell:

##        
##         CO2- CO2+
##   Temp-    6    4
##   Temp+    6    5

And here are the two tables with the order of Temp and CO2 reversed in the model

Df Sum Sq Mean Sq F value Pr(>F)
Temp 1 62.25 62.25 18.44 0.00049
CO2 1 21.49 21.49 6.36 0.02190
Temp:CO2 1 6.38 6.38 1.89 0.18720
Df Sum Sq Mean Sq F value Pr(>F)
CO2 1 17.59 17.59 5.21 0.03561
Temp 1 66.14 66.14 19.59 0.00037
CO2:Temp 1 6.38 6.38 1.89 0.18720

Several observations are important.

  1. the statistics for the last row, which is the interaction, does not change.
  2. if these data were analyzed in the software package JMP, or SAS, or SSPS then order wouldn’t matter. Here is what the tables would look like
Sum Sq Df F value Pr(>F)
Temp 58.77 1 17.41 0.00064
CO2 19.93 1 5.90 0.02648
Temp:CO2 6.38 1 1.89 0.18720
Sum Sq Df F value Pr(>F)
CO2 19.93 1 5.90 0.02648
Temp 58.77 1 17.41 0.00064
CO2:Temp 6.38 1 1.89 0.18720
  1. Order does not change the statistics in the coefficient table, even for unbalanced data:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.50 0.407 23.367 0.0000
Temp1 -1.70 0.407 -4.172 0.0006
CO21 0.99 0.407 2.430 0.0265
Temp1:CO21 -0.56 0.407 -1.374 0.1872
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.50 0.407 23.367 0.0000
CO21 0.99 0.407 2.430 0.0265
Temp1 -1.70 0.407 -4.172 0.0006
CO21:Temp1 -0.56 0.407 -1.374 0.1872

16.4.1 What is going on in unbalanced ANOVA? – Type I, II, III sum of squares

Type I sum of squares. Here is the (default) ANOVA table using Type I sum of squares for the urchin data with the three missing rows.

Df Sum Sq Mean Sq F value Pr(>F)
Temp 1 62.248 62.248 18.4 0.0005
CO2 1 21.488 21.488 6.4 0.0219
Temp:CO2 1 6.377 6.377 1.9 0.1872
Residuals 17 57.399 3.376

The default coding of dummy variables in R’s lm function is dummy coding, which is the coding used for Type I or Sequential Sum of Squares. The hypothesis tested by each row in the ANOVA table using Type I sum of squares is the effect of that row’s term conditional on all terms before it in the model (or above it in the table) and ignoring all terms after it in the model (or below it in the table).

  1. The hypothesis tested by the \(p\)-value for \(Temp\) is the same as if \(Temp\) were the only term in the model (other than the intercept). That is, the means are estimated for each level of \(Temp\) ignoring the fact that half the replicates within each level of \(Temp\) experienced low \(CO2\) and half experienced high \(CO2\)

  2. The hypothesis tested by the \(p\)-value for \(CO2\) is conditional on \(Temp\). That is, the difference in metabolism between \(CO2+\) and \(CO2-\) when \(Temp\) is “held constant” (or for all cases where \(Temp\) takes the same value). This is equivalent to the hypothesis that the difference in the marginal means of CO2 is zero.

  3. The hypothesis tested by the \(p\)-value for the interaction is conditional on all other terms and nothing is ignored.

Type II sum of squares. Here is the ANOVA table using Type II sum of squares for the urchin data with missing values. The interaction term is excluded from the linear model, because type II sum of squares are used to estimate main effects ignoring the interaction (so this would make sense only if a plot of the effects suggested a small interaction relative to the main effects). The sum of squares for the main effects would be the same if the interaction were included but the residual df, and thus the F and P-values would differ.

Df Sum Sq Mean Sq F value Pr(>F)
Temp 1 66.145 66.145 18.7 0.0004
CO2 1 21.488 21.488 6.1 0.0241
Residuals 18 63.776 3.543

The hypothesis tested by each row in the ANOVA table using Type II sum of squares is the effect of that row’s term conditional on all terms at the same level or below but ignoring all terms at a higher level in the model (or below it in the table). For example, the hypothesis test for a factor is conditioned on other factors but ignores interaction terms among the factors. Consequently, these hypotheses tested are

  1. The hypothesis tested by the \(p\)-value for \(Temp\) is conditional on \(CO2\). This is the same hypothesis that would occur using Type I sum of squares but placing \(Temp\) second in the model, after \(CO2\) (and it is in fact how I computed it for the table).

  2. The hypothesis tested by the \(p\)-value for \(CO2\) is conditional on \(Temp\). This is exactly the hypothesis for \(CO2\) using the Type I sum of squares above.

Type III sum of squares. Here is the ANOVA table using Type III sum of squares for the urchin data for missing data. The interaction term is excluded from the linear model, and advocates of using Type III sum of squares explicitly want this in the model.

Sum Sq Df F value Pr(>F)
Temp 58.770 1 17.406 0.0006
CO2 19.935 1 5.904 0.0265
Temp:CO2 6.377 1 1.889 0.1872
Residuals 57.399 17

The hypothesis tested by each row in the ANOVA table using Type III sum of squares is the effect of that row’s term conditional on all terms in the model.

  1. The hypothesis tested by the \(p\)-value for \(Temp\) is conditional on \(CO2\) and \(Temp:CO2\).

  2. The hypothesis tested by the \(p\)-value for \(CO2\) is conditional on \(Temp\) and \(Temp:CO2\).

  3. The hypothesis tested by the \(p\)-value for \(Temp:CO2\) is conditional on \(Temp\) and \(CO2\). This is the same for Type I sum of squares (and Type II, if the interaction term were included)

16.4.2 Back to interpretation of main effects

16.4.3 The anova tables for Type I, II, and III sum of squares are the same if the design is balanced.

16.5 Working in R

16.5.1 Type I sum of squares in R

The base R function anova() computes the ANOVA table using Type I sum of squares for any fit model object, such as that returned by lm. Here is a script for the urchin data. I first create unbalanced data by deleting the first row that is the control row.

cn_rows <- which(urchin[, Temp]=="Temp-" & urchin[, CO2]=="CO2-") # gives the rows of the controls
urchin_unbalanced <- urchin[-cn_rows[1],] # deletes the row that is in first element of cn_rows
urchin.t1 <- lm(Resp ~ Temp*CO2, data=urchin_unbalanced)
anova(urchin.t1)
## Analysis of Variance Table
## 
## Response: Resp
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## Temp       1 55.696  55.696 16.9244 0.0005907 ***
## CO2        1 18.411  18.411  5.5946 0.0288072 *  
## Temp:CO2   1  9.204   9.204  2.7970 0.1108298    
## Residuals 19 62.527   3.291                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

16.5.2 Type II and III Sum of Squares

Type II sum of squares can be computed manually simply by fitting the model twice, once with the factors ordered one way and then with the factors ordered the opposite way. The car package has the function Anova that specifically outputs Type II and Type III ANOVA tables.

Type II sum of squares can be fit with the interaction in the model, and this generates the Type II sum of squares for the main terms but the residual is wrong for the \(F\)-ratio because it is the residual from the full model and Type II assumes the interaction effect is zero. So, if one wants an ANOVA table with a \(F\) and \(p\) that reflect this, then the interaction should be dropped from the model.

urchin.t2 <- lm(Resp ~ Temp*CO2, data=urchin_unbalanced)
Anova(urchin.t2, type="2")
## Anova Table (Type II tests)
## 
## Response: Resp
##           Sum Sq Df F value    Pr(>F)    
## Temp      52.711  1 16.0173 0.0007624 ***
## CO2       18.411  1  5.5946 0.0288072 *  
## Temp:CO2   9.204  1  2.7970 0.1108298    
## Residuals 62.527 19                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
urchin.t2 <- lm(Resp ~ Temp + CO2, data=urchin_unbalanced)
Anova(urchin.t2, type="2")
## Anova Table (Type II tests)
## 
## Response: Resp
##           Sum Sq Df F value   Pr(>F)   
## Temp      52.711  1 14.6968 0.001038 **
## CO2       18.411  1  5.1333 0.034725 * 
## Residuals 71.731 20                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

To get type III sum of squares, we need to specify effects coding for the model matrix. The safest way to do this is something like this

con3 <- list(Temp=contr.sum, CO2=contr.sum) # change the contrasts coding for the model matrix
urchin.t3 <- lm(Resp ~ Temp*CO2, data=urchin_unbalanced, contrasts=con3)
Anova(urchin.t3, type="3")
## Anova Table (Type III tests)
## 
## Response: Resp
##              Sum Sq Df  F value    Pr(>F)    
## (Intercept) 2148.60  1 652.8939 3.559e-16 ***
## Temp          54.71  1  16.6241 0.0006422 ***
## CO2           17.15  1   5.2119 0.0341221 *  
## Temp:CO2       9.20  1   2.7970 0.1108298    
## Residuals     62.53 19                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1